Теоремы о непрерывности и дифференцируемости сложной функции
Теорема 1.Пусть сложная функция 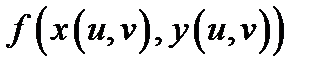 определена в точке
определена в точке  и некоторой ее окрестности и пусть выполнены условия: а) функции
и некоторой ее окрестности и пусть выполнены условия: а) функции 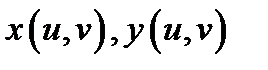 непрерывны в точке
непрерывны в точке  б) функция
б) функция 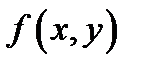 непрервына в соответствующей точке
непрервына в соответствующей точке 
Тогда сложная функция 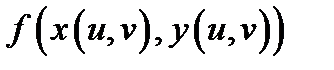 непрерывна в точке
непрерывна в точке 
Теорема 2.Пусть сложная функция 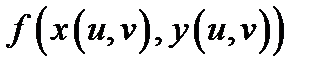 определена в точке
определена в точке  и некоторой ее окрестности и пусть выполнены условия: а) функции
и некоторой ее окрестности и пусть выполнены условия: а) функции 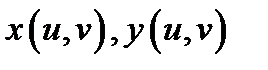 дифференцируемы в точке
дифференцируемы в точке  б) функция
б) функция 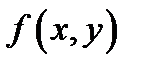 дифференцируема в соответствующей точке
дифференцируема в соответствующей точке  Тогда сложная функция
Тогда сложная функция 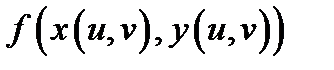 дифференцируема в точке
дифференцируема в точке 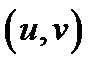 и имеют место равенства
и имеют место равенства
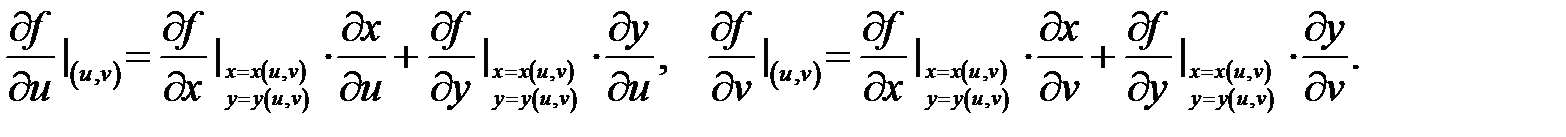
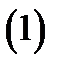
В случае, когда внутренние функции 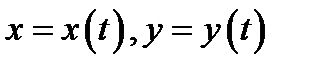 зависят от одной переменной, сложная функция
зависят от одной переменной, сложная функция 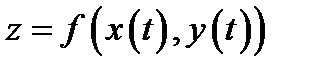 является также функцией одной переменной; при этом
является также функцией одной переменной; при этом
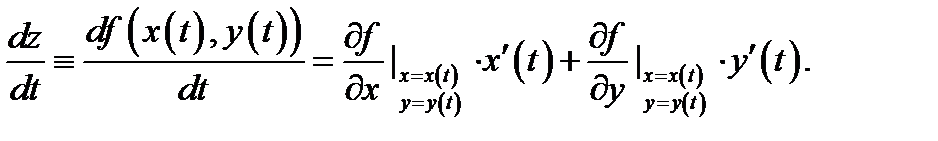

Доказательствопроведем для второго случая. Так как функция 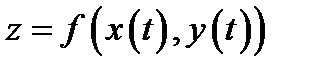 дифференци-
дифференци-
руема в точке 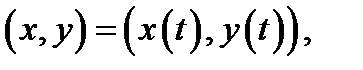 то имеет место представление
то имеет место представление

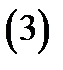
С другой стороны, так как функции 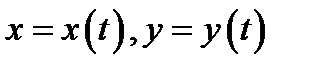 дифференцируемы в рассматриваемой точке
дифференцируемы в рассматриваемой точке  то имеют место асимптотические разложения
то имеют место асимптотические разложения
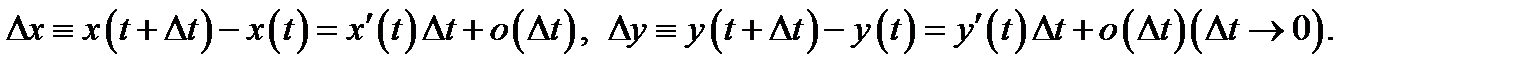
Подставляя это в (3) (при этом учитываем, что при 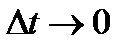 приращения
приращения 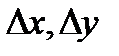 также стремятся к нулю, а значит,
также стремятся к нулю, а значит, 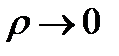 ), будем иметь
), будем иметь
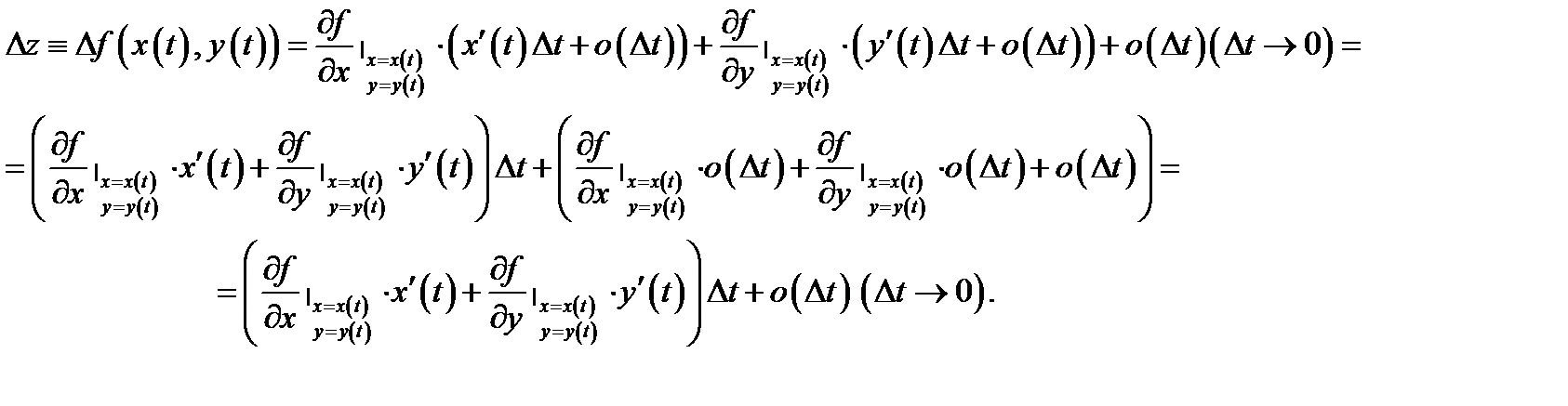
Это означает, что функция 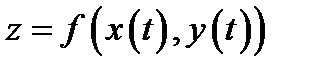 дифференцируема в точке
дифференцируема в точке  и что имеет место равенство (2). Теорема доказана.
и что имеет место равенство (2). Теорема доказана.
Например, если  то
то  поэтому
поэтому
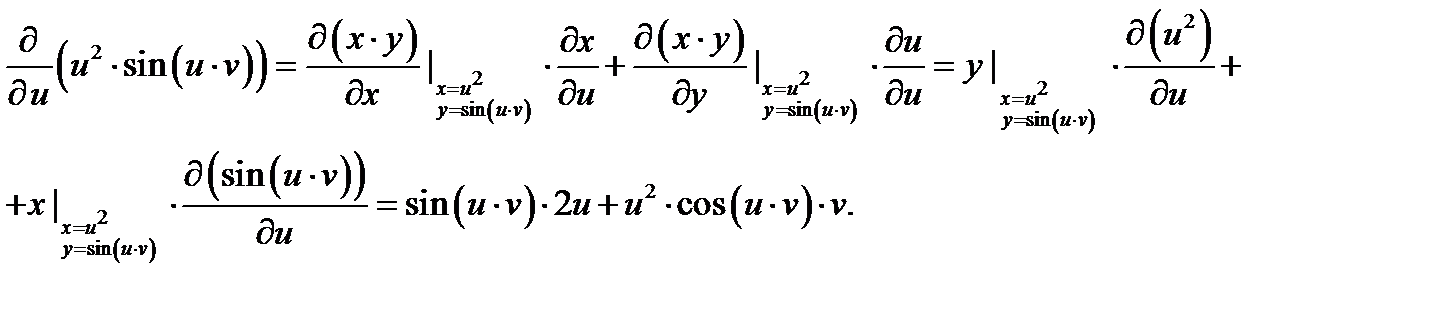
Аналогично вычисляем 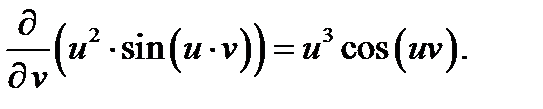
Дата добавления: 2017-03-29; просмотров: 1014;
