Частные производные и дифференциалы высших порядков. Равенство смешанных производных
Если функции 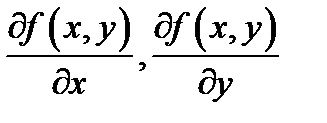 дифференцируемы в точке
дифференцируемы в точке 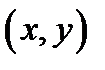 и некоторой ее окрестности, то функции
и некоторой ее окрестности, то функции
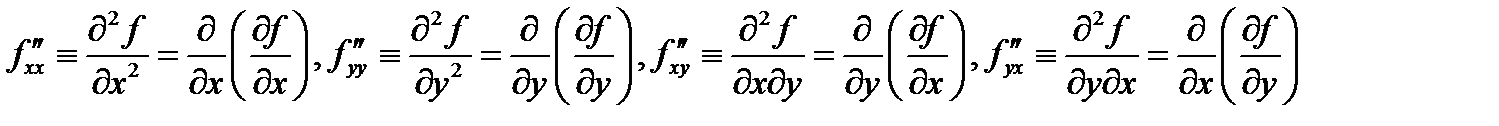
называются вторыми частными производными функции 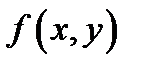 в точке
в точке 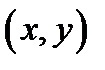 (при этом производные
(при этом производные 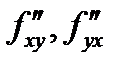 называются смешанными производным). Аналогично определяются частные производные более высокого порядка. Например,
называются смешанными производным). Аналогично определяются частные производные более высокого порядка. Например,

Если функция 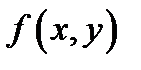 непрерывна в точке
непрерывна в точке 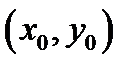 и имеет в этой точке непрерывные частные производные до
и имеет в этой точке непрерывные частные производные до 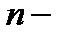 порядка включительно, то её называют
порядка включительно, то её называют 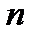 раз дифференцируемой в этой точке.
раз дифференцируемой в этой точке.
Имеет место следующее утверждение.
Теорема 5(о равенстве смешанных производных). Пусть в точке 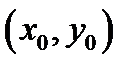 и в некоторой ее окрестности существуют частные производные
и в некоторой ее окрестности существуют частные производные 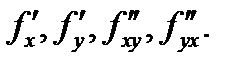 Тогда если смешанные производные
Тогда если смешанные производные
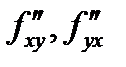 непрерывны в точке
непрерывны в точке  то они совпадают в этой точке:
то они совпадают в этой точке: 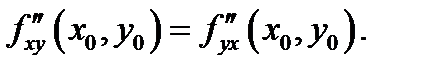 Аналогичное утверждение имеет место и для смешанных производных более высокого порядка (например,
Аналогичное утверждение имеет место и для смешанных производных более высокого порядка (например, 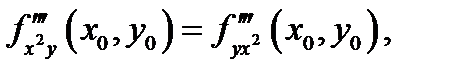 если частные производные
если частные производные  непрерывны в точке
непрерывны в точке 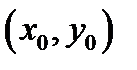 ).
).
Пример 1.Найти вторые смешанные производные для функции 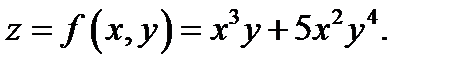
Решение.Имеем
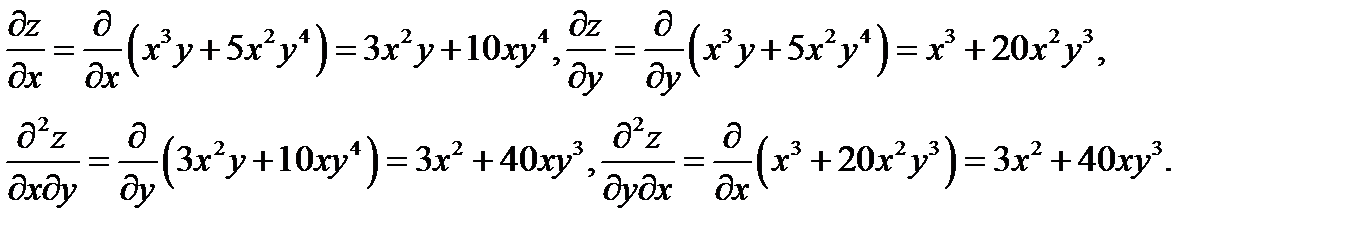

По аналогии с дифференциалами высших порядков функции одной переменной определяются и дифференциалы высших порядков для функций многих переменных. А именно, если известен дифференциал 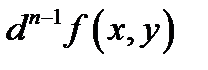 порядка
порядка 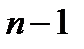 , то дифференциал
, то дифференциал  го порядка определяется по индукции:
го порядка определяется по индукции: 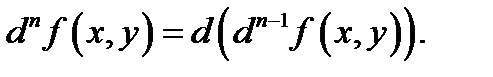 При этом дифференциалы независимых переменных
При этом дифференциалы независимых переменных 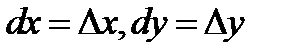 и их степени
и их степени 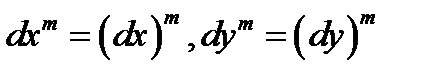 считаются постоянными дифференцирования.
считаются постоянными дифференцирования.
 Если функция
Если функция 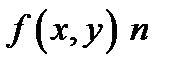 раз дифференцируема в точке
раз дифференцируема в точке  то ее дифференциал
то ее дифференциал 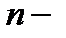 порядка в этой точке вычисляется по формуле
порядка в этой точке вычисляется по формуле
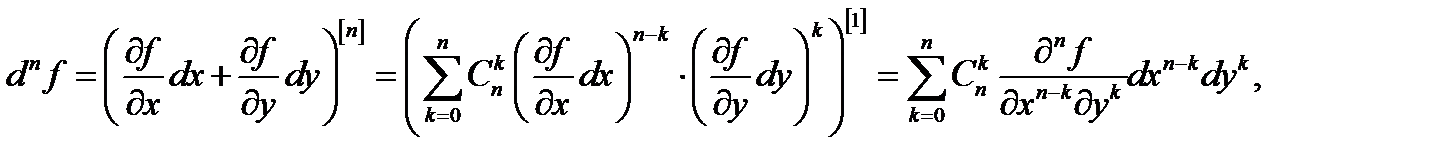
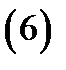
где  символ
символ 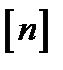 означает, что надо сначала выражение
означает, что надо сначала выражение 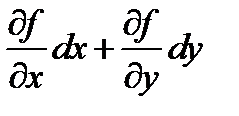 возвести в
возвести в 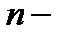 ую степень[3], а затем произведения вида
ую степень[3], а затем произведения вида  заменить на частные производные
заменить на частные производные 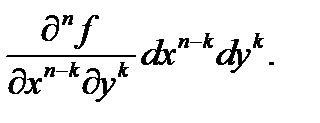 Например,
Например,
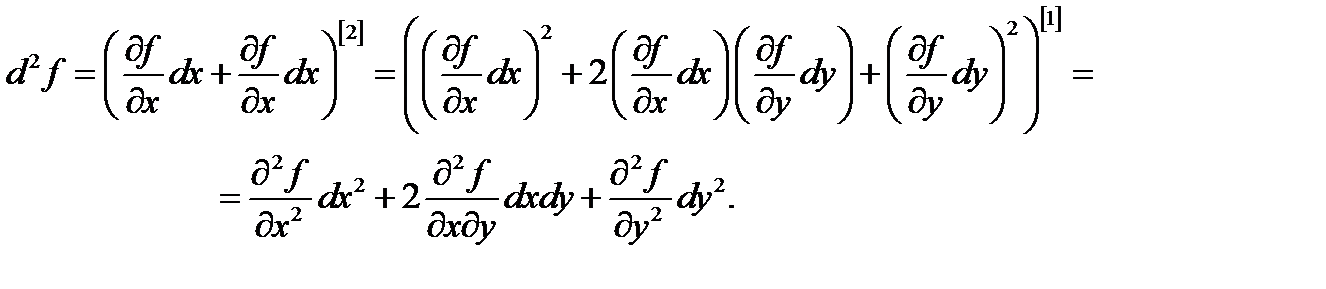

С помощью дифференциалов высших порядков можно в краткой форме записать формулу Тейлора для функций многих переменных.
Теорема 7.Пусть в точке 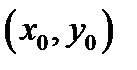 и некоторой её окрестности
и некоторой её окрестности 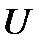 функция
функция 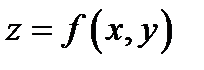 имеет непрерывные частные производные до
имеет непрерывные частные производные до 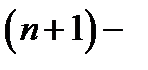 порядка включительно. Тогда для каждой точки
порядка включительно. Тогда для каждой точки 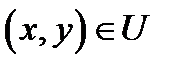 имеет место представление
имеет место представление
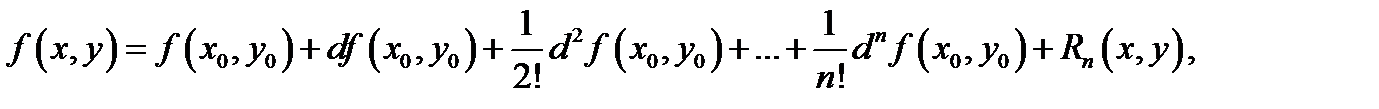
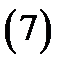
где 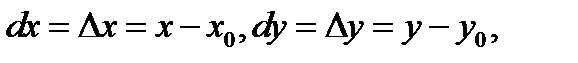 остаточный член
остаточный член 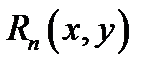 (в форме Лагранжа) имеет вид
(в форме Лагранжа) имеет вид 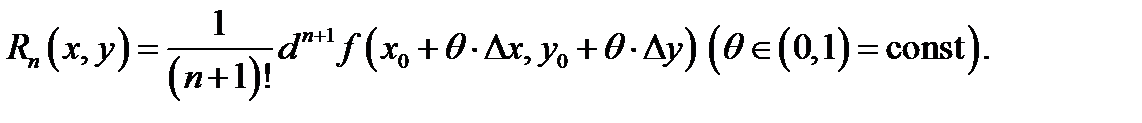
Дата добавления: 2017-03-29; просмотров: 1053;
