Постановка задачи и описание метода решения

Имеется выборка n значений входных переменных объекта x(i) и выходной переменной y(i), где i=t₀+∆t; t₀+2∆t;…. t₀+n∆t, i=1,2,….n – дискретные моменты времени, ∆t – интервалы времени проведения эксперимента.

Значения входных и входных переменных представлены матрицами:

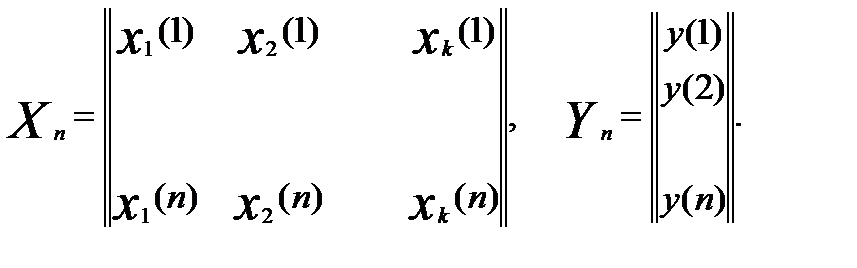(1)

Положим, что модель объекта имеет вид:

y(i)=B^T(i)x(i) + e(i), (2)

где B(i) – вектор действительных значений коэффициентов в момент времени i; x(i) – значение вектора входных переменных в момент i.

Последовательность значений B(i), x(i) являются случайными, стационарными и эргодическими. Ошибка e(i) является случайной нормально распределенной величиной с нулевым математическим ожиданием и дисперсией σ_е².

Значения коэффициентов изменяются во времени. Задача заключается в нахождении оценки B(n+α) в момент (n+α), где α=1,2,,… α<<<n. наилучшей оценки в определенном смысле. При α>0 наша задача является задачей прогнозирования значений коэффициентов, а при α=0 – задачей фильтрации. При объединении обеих случаев имеем задачу слежения за процессом изменения коэффициентов модели. Структура алгоритма вычисления оценок коэффициентов модели задается с точностью до некоторого небольшого числа параметров γ. Оптимальные свойства алгоритм достигаются выбором значений параметра γ. Одним из таких способов является метод «замороженных» коэффициентов или метод «скользящего интервала».

Будем рассматривать алгоритм вычисления оценок B(n+α), представленный в рекуррентной форме, связывающий оценку для момента (n+α) с ранее найденной оценкой для момента (n+α-1):

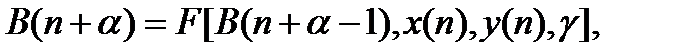(3)

где F – функция, определяющая структуру алгоритма; γ – параметр алгоритма.

Выбор наилучшего значения параметра γ проводится по имеющейся выборке. Используя алгоритм (3) получают последовательность оценок B(α+1), B(α+2), … B(α+n). Имея эту последовательность, вычисляется сумма квадратов ошибок слежения за измененяемым выходом объекта по выборке:

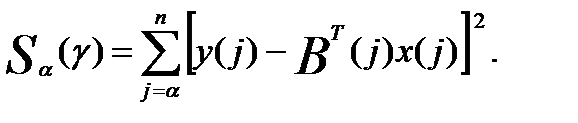(4)

Величина 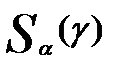используется в качестве критерия для нахождения оценки оптимальной величины γ.

Значения оценок коэффициентов модели вычисляются для момента времени (n+α)

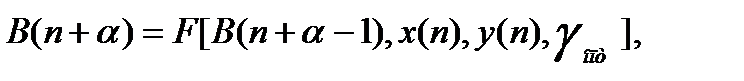
и в свою очередь

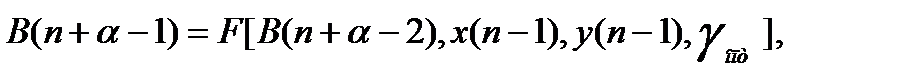и т.д.

Оценки параметров модели будут состоятельными, когда переходной процесс заканчивается за конечное число шагов m. Длительность переходного процесса m зависит от выбора начального приближения B(α). Переходный процесс практически будет отсутствовать, если оценка параметров будет вычисляться по выборке и станет близкой к истинной величине (при медленном характере дрейфа параметров).