Компонентный анализ
Компонентный анализ является методом определения структурной зависимости между случайными переменными [5]. Идея метода заключается в замене сильно коррелированных переменных новыми переменными (главными компонентами), между которыми корреляция отсутствует. В результате его использования получается сжатое описание малого объема, несущее почти всю информацию, содержащуюся в исходных данных. Главные компоненты получаются из исходных переменных путем целенаправленного вращения, т.е. как линейные комбинации исходных переменных. Вращение производится таким образом, чтобы главные компоненты были ортогональны и имели максимальную дисперсию среди возможных линейных комбинаций исходных переменных. При этом переменные не коррелированны между собой и упорядочены по убыванию дисперсии (первая компонента имеет наибольшую дисперсию). Кроме того, общая дисперсия после преобразования остается без изменений.
Ход рассуждений при выполнении поиска главных компонент заключается в следующем. Мы предполагаем наличие некоррелированных переменных Zj ( j=1…k), каждая из которых представляется нам комбинацией основных переменных (суммирование по i =1…k):
Zj = S Aj i ·X i
и, кроме того, обладает дисперсией, такой что
D(Z1) ³ D(Z2) ³ … ³ D(Zk).
Поиск коэффициентов Aj i(их называют весом j-й компоненты в содержании i-й переменной) сводится к решению матричных уравнений и не представляет особой сложности при использовании компьютерных программ. Но суть метода весьма интересна и на ней стоит задержаться.
Как известно из векторной алгебры, диагональная матрица [2·2] может рассматриваться как описание 2-х точек (точнее — вектора) в двумерном пространстве, а такая же матрица размером [k·k]—как описание k точек k-мерного пространства.
Так вот, замена реальных, хотя и нормированных переменных Xi на точно такое же количество переменных Z jозначает не что иное, как поворот kосей многомерного пространства.
“Перебирая” поочередно оси, мы находим вначале ту из них, где дисперсия вдоль оси наибольшая. Затемделаем пересчет дисперсий для оставшихсяk-1осей и снова находим “ось-чемпион” по дисперсии и т.д.
Образно говоря, мы заглядываем в куб (3-х мерное пространство) по очереди по трем осям и вначале ищем то направление, где видим наибольший “туман” (наибольшая дисперсия говорит о наибольшем влиянии чего-то постороннего); затем “усредняем” картинку по оставшимся двум осям и сравниваем разброс данных по каждой из них — находим “середнячка” и “аутсайдера”. Теперь остается решить систему уравнений — в нашем примере для 9 переменных, чтобы отыскать матрицу коэффициентов (весов) A[k·k].
Если коэффициенты Aj i найдены, то можно вернуться к основным переменным, поскольку доказано, что они однозначно выражаются в виде (суммирование по j=1…k)
X i = S Aji·Z j .
Отыскание матрицы весов A[k·k]требует использования ковариационной матрицы и корреляционной матрицы.
Таким образом, метод главных компонент отличается прежде все тем, что дает всегда единственное решение задачи. Правда, трактовка этого решения своеобразна.
1) Мы решаем задачу о наличии ровно стольких факторов, сколько у нас наблюдаемых переменных, т.е. вопрос о нашем согласии на меньшее число латентных факторов невозможно поставить;
2) В результате решения, теоретически всегда единственного, а практически связанного с громадными вычислительными трудностями при разных физических размерностях основных величин, мы получим ответ примерно такого вида — фактор такой-то (например, привлекательность продавцов при анализе дневной выручки магазинов) занимает третье место по степени влияния на основные переменные.
Этот ответ обоснован — дисперсия этого фактора оказалась третьей по крупности среди всех прочих. Больше ничего получить в этом случае нельзя. Другое дело, что этот вывод оказался нам полезным или мы его игнорируем — это наше право решать, как использовать системный подход.
Пример. Имеются данные, описывающие зависимость результирующей переменной «y» от факторных переменных x1 – x3 (таблица 5).
Требуется выделить главные компоненты и построить уравнение регрессии на главных компонентах.
Перед тем как проводить компонентный анализ, проводится анализ независимости исходных признаков. Проверяется значимость матрицы парных корреляций с помощью критерия Уилкса.
Выдвигается гипотеза: Н0: 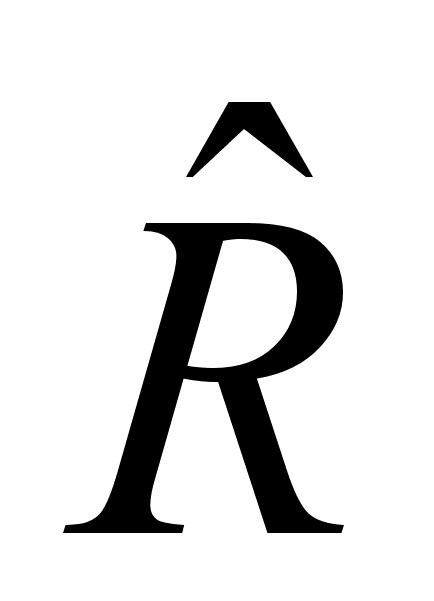 незначима и альтернативная Н1:
незначима и альтернативная Н1: 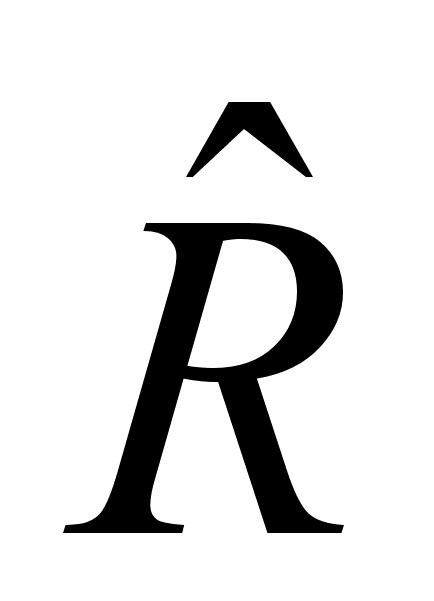 значима.
значима.
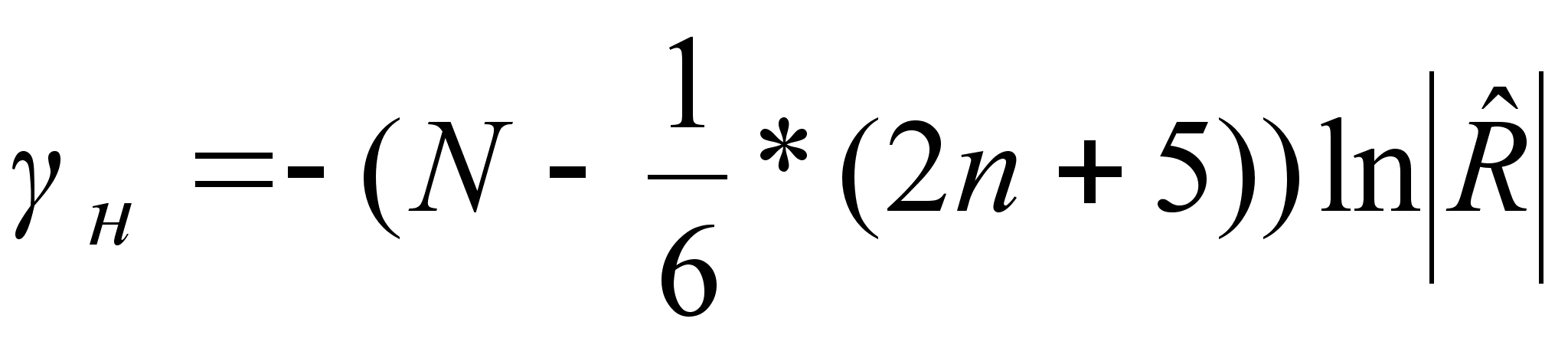
Рассчитывается статистика, которая распределена по закону 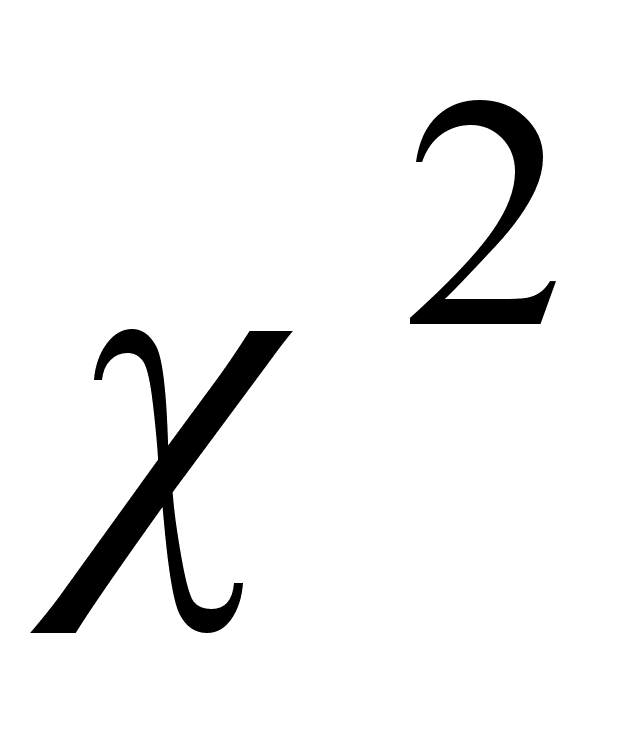 с
с 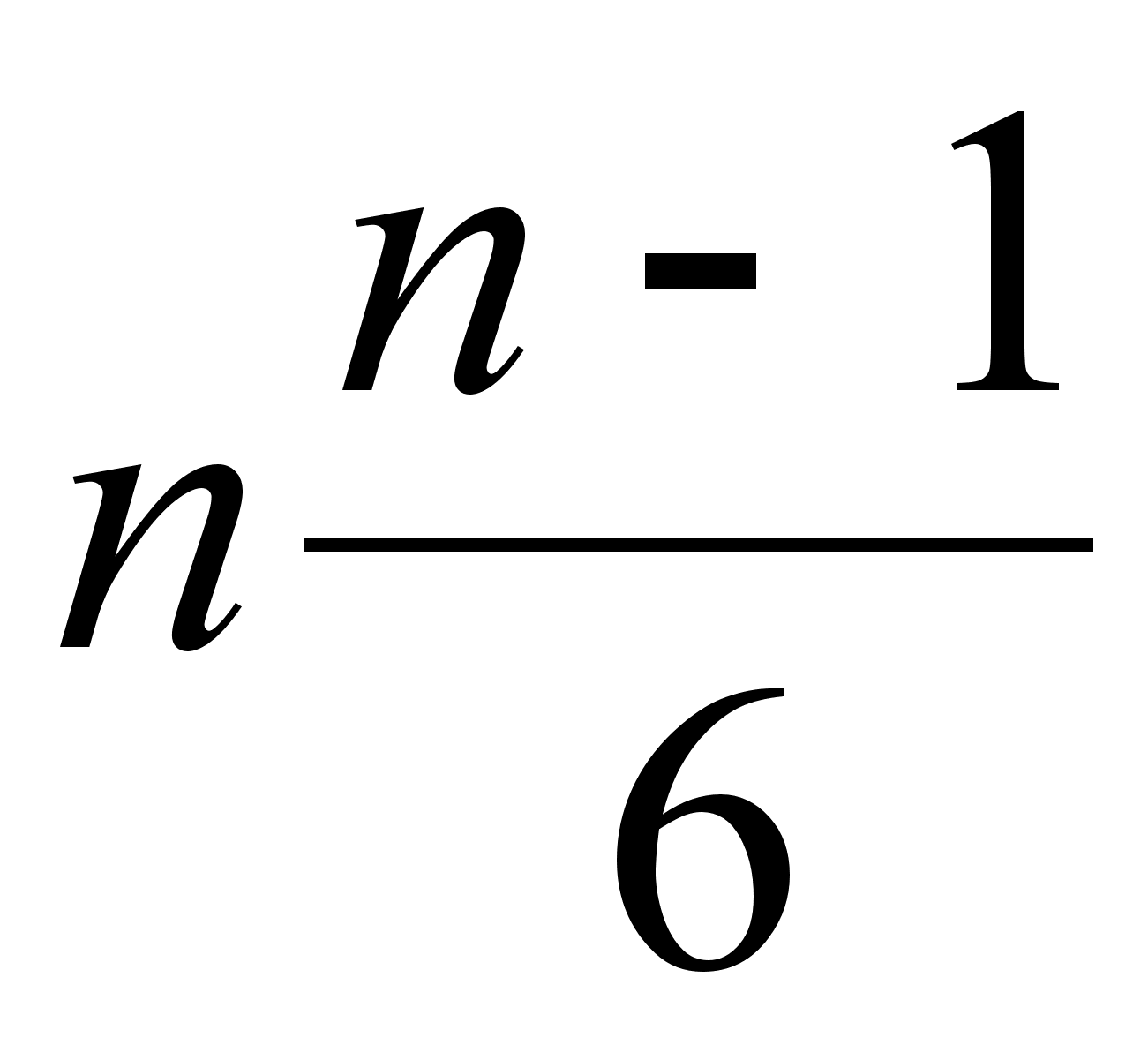 - степенями свободы. Сравнивается расчетное значение с табличным значением
- степенями свободы. Сравнивается расчетное значение с табличным значением 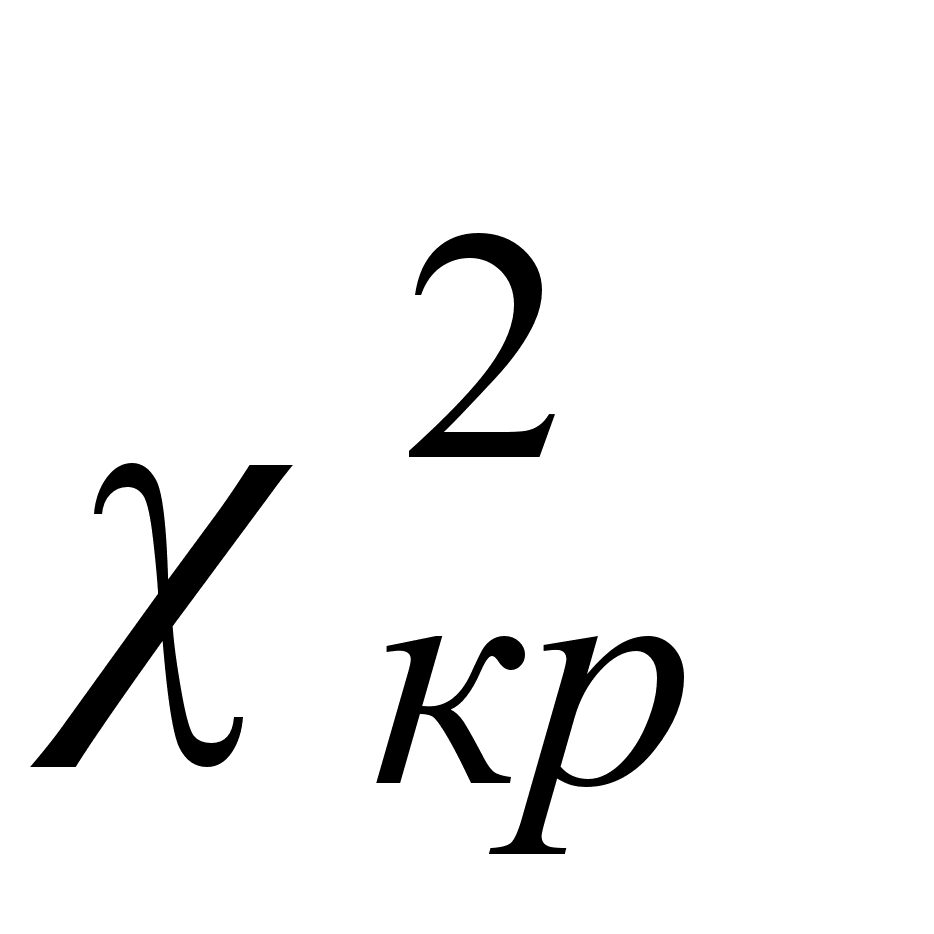 для уровня значимости α = 0,05.
для уровня значимости α = 0,05.
Таблица 5- Зависимость результирующей переменной
от факторных переменных
| х1 | х2 | х3 | у |
| 1,1 | 1,1 | 1,2 | 26,2 |
| 1,4 | 1,5 | 1,1 | 25,9 |
| 1,7 | 1,8 | 32,5 | |
| 1,7 | 1,7 | 1,8 | 31,7 |
| 1,8 | 1,9 | 1,8 | 31,7 |
| 1,8 | 1,8 | 1,9 | 33,6 |
| 1,9 | 1,8 | 34,2 | |
| 2,1 | 2,1 | 34,4 | |
| 2,3 | 2,4 | 2,5 | 35,5 |
| 2,5 | 2,5 | 2,4 | 36,5 |
Если расчетное значения критерия будет больше табличного значения
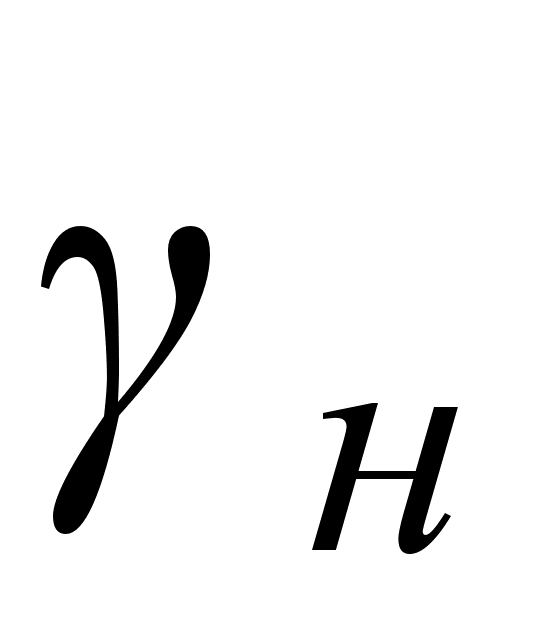 >
> 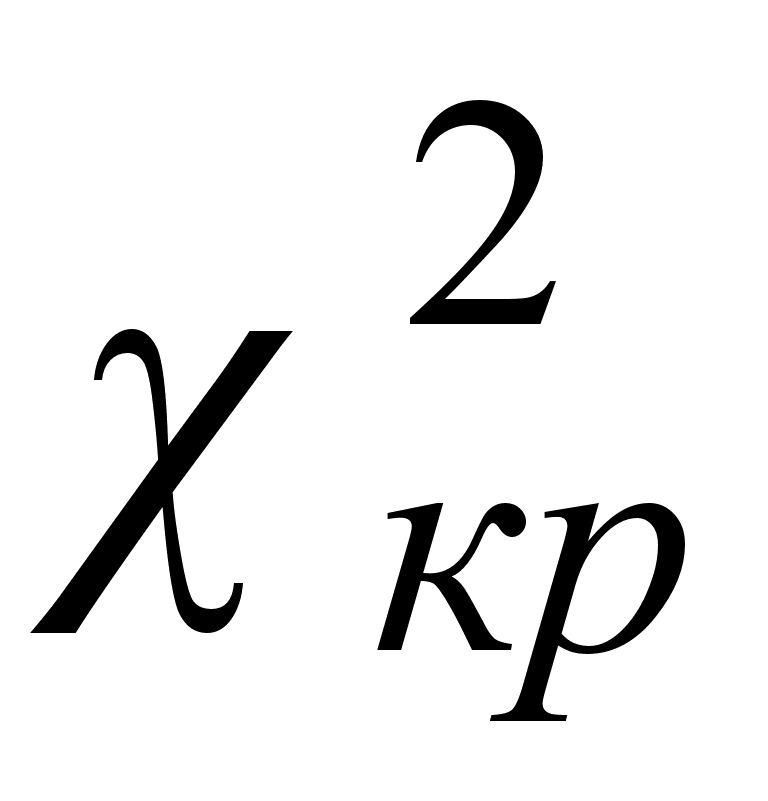 , то гипотеза Н0 отвергается и принимается альтернативная Н1:
, то гипотеза Н0 отвергается и принимается альтернативная Н1: 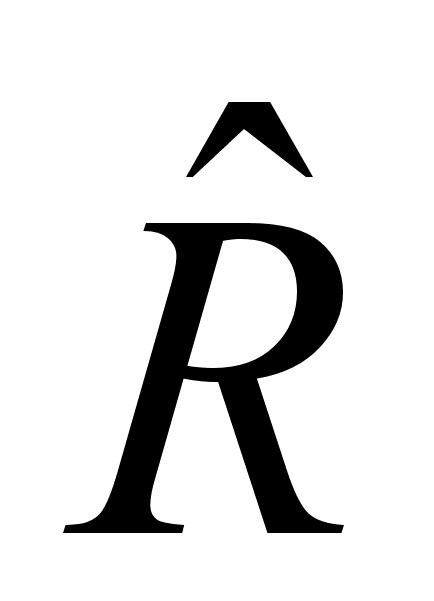 значима, следовательно, имеет смысл проводить компонентный анализ.
значима, следовательно, имеет смысл проводить компонентный анализ.
Затем поверяется гипотеза о диагональности ковариационной матрицы.
Выдвигается нулевая гипотеза:
Н0: соv 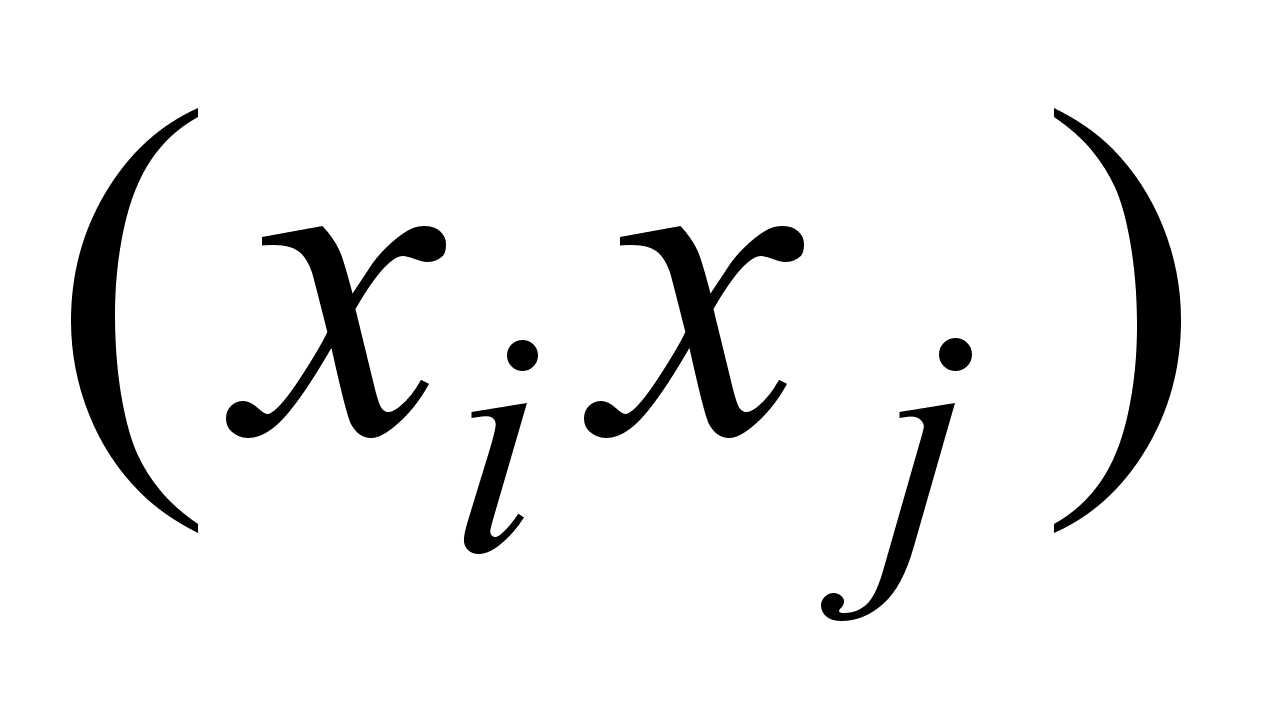 =0,
=0, 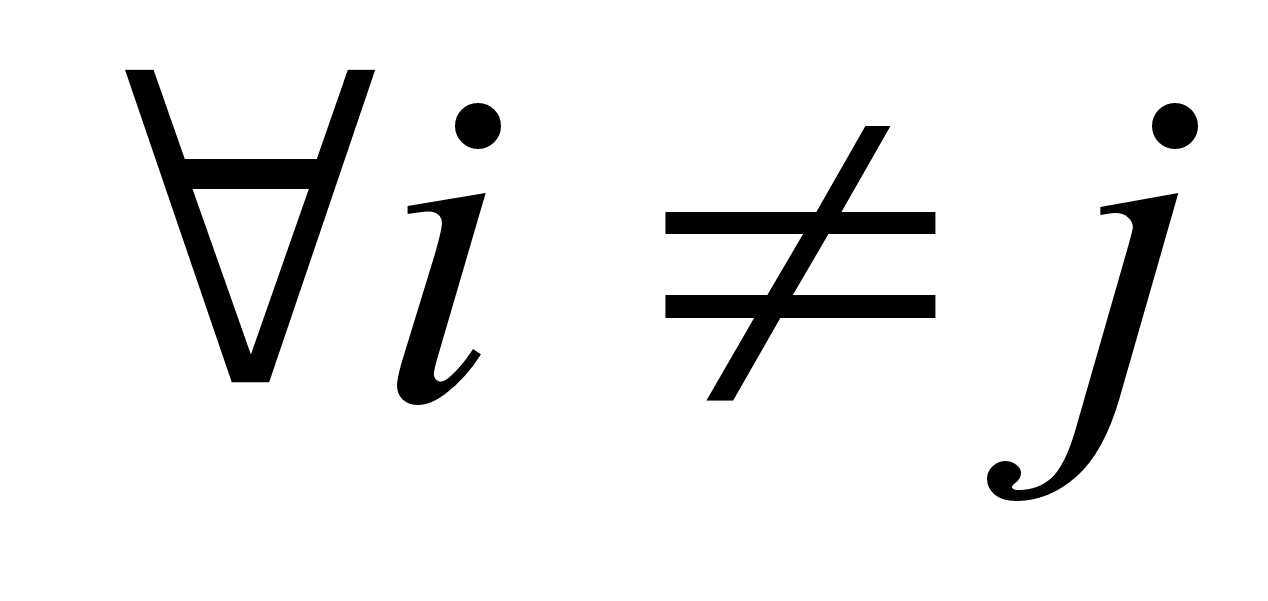 и альтернативная Н1: соv
и альтернативная Н1: соv 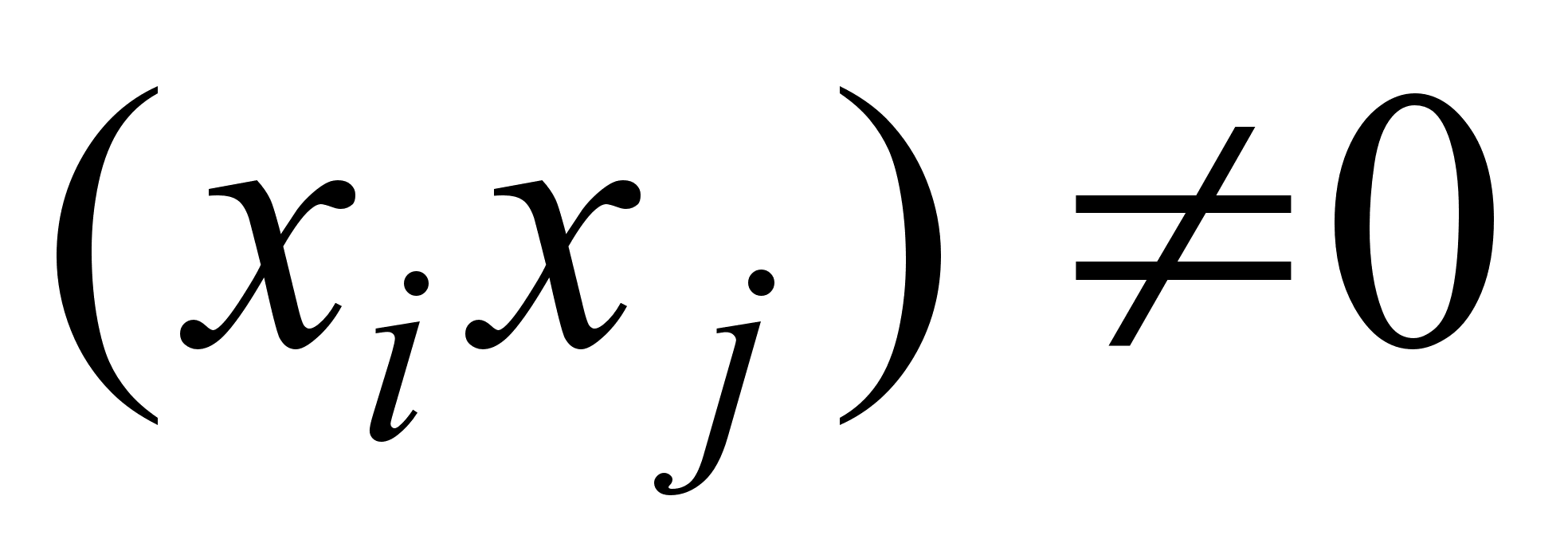 .
.
Рассчитывается статистика 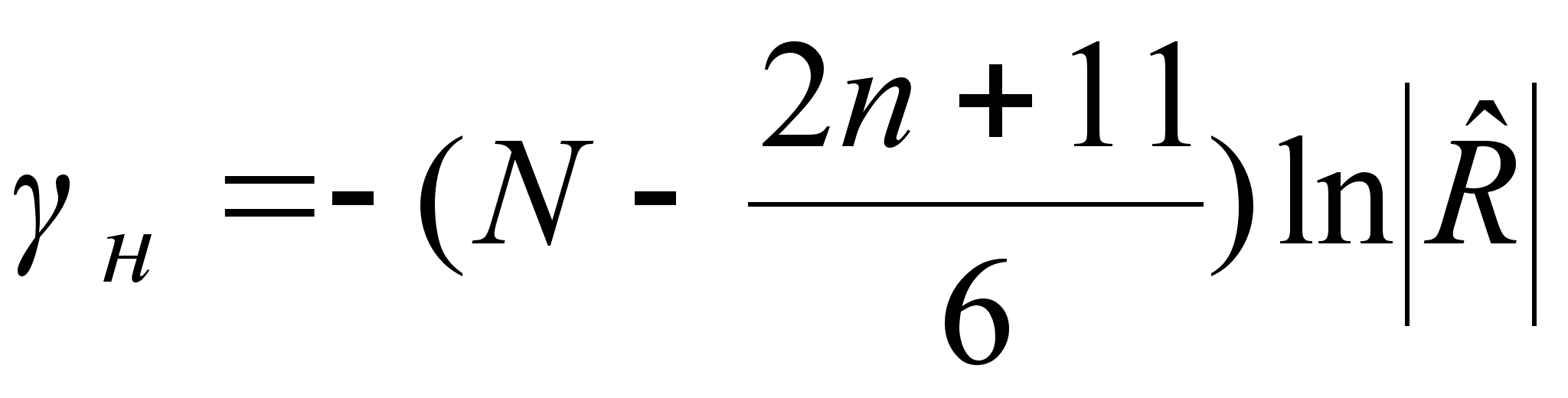 , которая распределяется по закону
, которая распределяется по закону 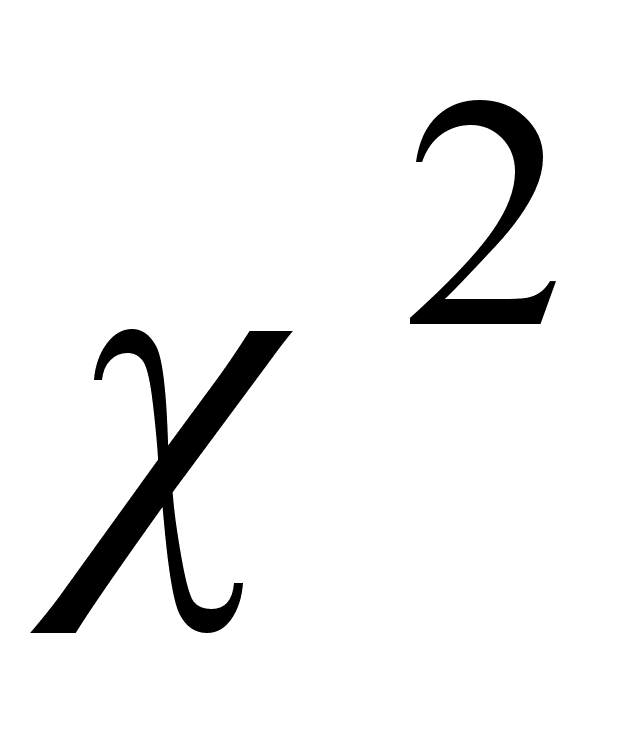 с
с 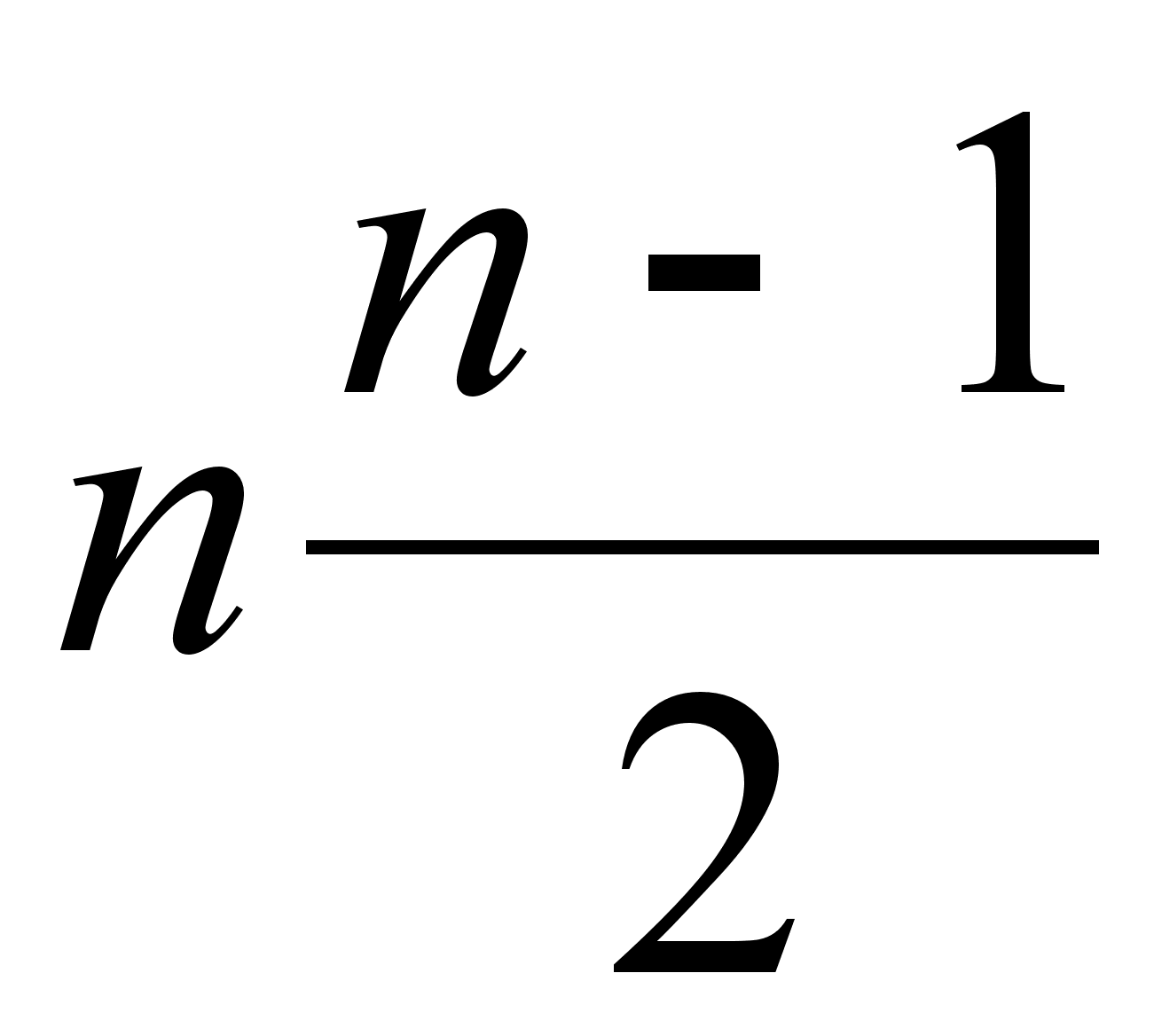 степенями свободы.
степенями свободы.
Если расчетное значения критерия будет больше табличного значения
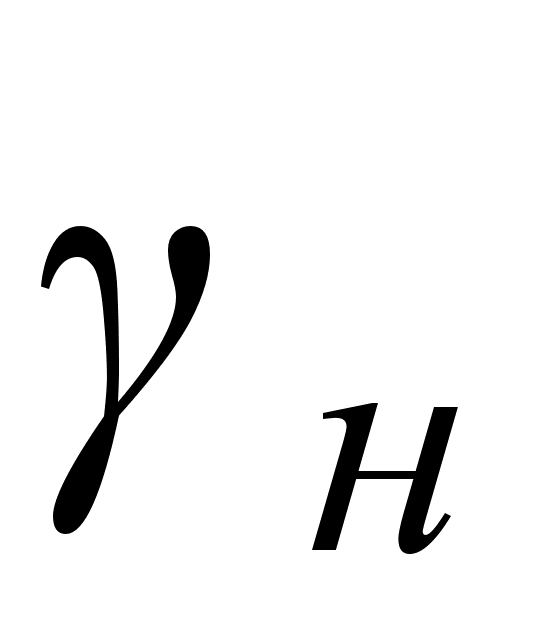 >
> 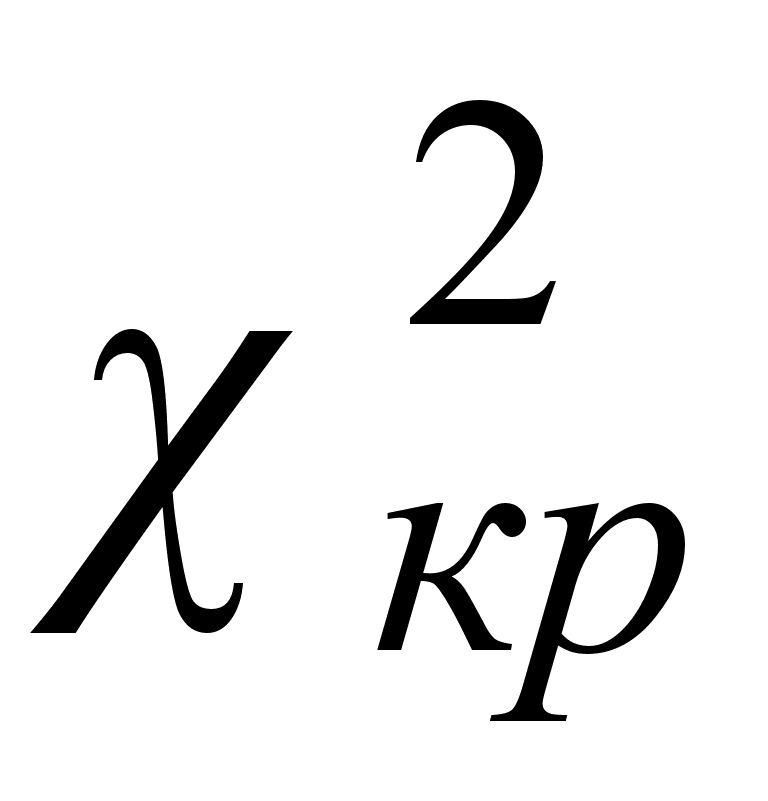 , то гипотеза Н0 отвергается и принимается альтернативная Н1:
, то гипотеза Н0 отвергается и принимается альтернативная Н1: 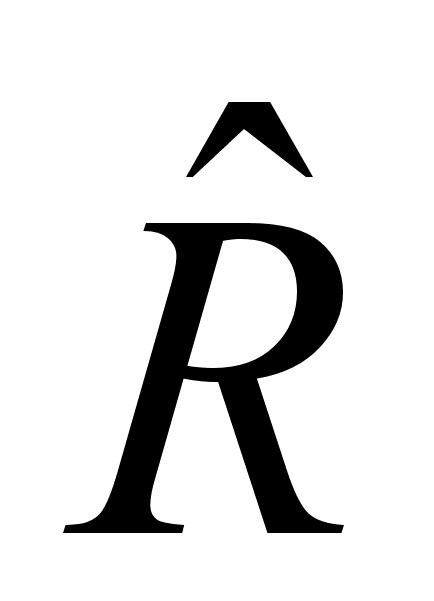 значима, что подтверждает мультиколлениарность данных, следовательно имеет смысл проводить компонентный анализ.
значима, что подтверждает мультиколлениарность данных, следовательно имеет смысл проводить компонентный анализ.
Анализ данных (табл.5) выявил значимую коррелированность переменных x1 – x3, что подтверждает целесообразность проведения компонентного анализа.
Компонентный анализ проводим с использованием ППП Statgraphics Plus. Для получения данных компонентного анализа вызываем подменю Tabular optionsипомечаем окно Analysis Summaru. Результаты анализа приведены в таблице 6.
| Principal Components Analysis -------------------------------------------------- Component Percent of Cumulative Number Eigenvalue Variance Percentage 1 2,888 96,26 96,26 2 0,0985 3,28 99,54 3 0,0137 0,45 100,00 -------------------------------------------------- |
На уровне информативности 95% и выше выделяется одна главная компонента. Она имеет наибольшую дисперсию, равную 96,26%. Использование второй главной компоненты не приводит к существенному увеличению дисперсии (всего на 3,28%).
Программа рассчитывает значения главных компонент для всех опытных данных. Используя значения главных компонент строим регрессионное уравнение:
| y = 32,22 + 2,00 z1. |
Первая главная компонента z1 адекватно описывает зависимую переменную y. Коэффициент детерминации равен R2 = 89,34%, статистически значим при уровне значимости 0,05. Стандартная ошибка модели равна 1,25.
Факторный анализ
Факторный анализ служит для выявления и обоснования действия различных признаков и их комбинаций на исследуемый процесс путем снижения их размерности [5]. Такая задача решается, как правило, путем "сжатия" исходной информации и выделения из нее наиболее "существенной" информации. Объект описывается меньшим числом обобщенных признаков, называемых факторами.
При использовании методов факторного анализа решаются следующие задачи:
- отыскание скрытых, но объективно существующих закономерностей исследуемого процесса, определяемых воздействием внутренних и внешних причин;
- описание изучаемого процесса значительно меньшим числом факторов по сравнению с первоначально взятым количеством признаков;
- выявление первоначальных признаков, наиболее тесно связанных с основными факторами;
- прогнозирование процесса на основе уравнения регрессии, построенного по полученным факторам.
Несколько иначе осуществляется исследование латентных переменных в случае применения факторного анализа. Здесь каждая реальная переменная рассматривается также как линейная комбинация ряда факторов Fj , но в несколько необычной форме:
X i = S B ji · Fj + D i.
причем суммирование ведется по j=1…m , т.е. по каждому фактору.
Здесь коэффициент Bji принято называть нагрузкой на j-й фактор со стороны i-й переменной, а последнее слагаемое D i рассматривать как помеху, случайное отклонение для Xi.Число факторов m вполне может быть меньше числа реальных переменных n и ситуации, когда мы хотим оценить влияние всего одного фактора (ту же вежливость продавцов), здесь вполне допустимы.
Обратим внимание на само понятие “латентный”, скрытый, непосредственно не измеримый фактор. Конечно же, нет прибора и нет эталона вежливости, образованности, выносливости и т.п. Но это не мешает нам самим “измерить” их — применив соответствующую шкалу для таких признаков, разработав тесты для оценки таких свойств по этой шкале и применив эти тесты к тем же продавцам.
Так в чем же тогда “ненаблюдаемость”? А в том, что в процессе эксперимента (обязательно) массового мы не можем непрерывно сравнивать все эти признаки с эталонами. Нам приходится брать предварительные, усредненные, полученные совсем не в “рабочих” условиях данные.
Можно отойти от экономики и обратиться к спорту. Кто будет спорить, что результат спортсмена при прыжках в высоту зависит от фактора — “сила толчковой ноги”. Да, это фактор можно измерить и в обычных физических единицах (ньютонах или бытовых килограммах), но когда?! Не во время же прыжка на соревнованиях!
А ведь именно в это, рабочее время фиксируются статистические данные, накапливается материал для исходной матрицы.
Несколько более сложно объяснить сущность самих процедур факторного анализа простыми, элементарными понятиями (по мнению некоторых специалистов в области факторного анализа — вообще невозможно). Поэтому постараемся разобраться в этом, используя достаточно сложный, но, к счастью, доведенный в практическом смысле до полного совершенства, аппарат векторной или матричной алгебры.
До того как станет понятной необходимость в таком аппарате, рассмотрим так называемую основную теорему факторного анализа. Суть ее основана на представлении модели факторного анализа в матричном виде:
X [k·1] = B [k·m] · F [m·1] + D [k·1]
и на последующем доказательстве истинности выражения
R [k·k] = B [k·m] · Bт[m·k],
для “идеального” случая, когда невязки Dпренебрежимо малы.
Здесь Bт[m·k]это та же матрица B [k·m], но преобразованная особым образом (транспонированная).
Трудность задачи отыскания матрицы нагрузок на факторы очевидна — еще в школьной алгебре указывается на бесчисленное множество решений системы уравнений, если число уравнений больше числа неизвестных. Грубый подсчет говорит, что нам понадобится найти k·m неизвестных элементов матрицы нагрузок, в то время как известно около k2 / 2 коэффициентов корреляции. Некоторую “помощь” оказывает доказанное в теории факторного анализа соотношение между данным коэффициентом парной корреляции (например, R12) и набором соответствующих нагрузок факторов:
R12 = B11 · B21 + B12 · B22 + … + B1m · B2m .
Таким образом, нет ничего удивительного в том утверждении, что факторный анализ (а, значит, и системный анализ в современных условиях) — больше искусство, чем наука. Здесь менее важно владеть “навыками” и крайне важно понимать как мощность, так и ограниченные возможности этого метода.
Есть и еще одно обстоятельство, затрудняющее профессиональную подготовку в области факторного анализа — необходимость быть профессионалом в “технологическом” плане, в нашем случае в предметной области.
Но, с другой стороны, стать профессионалом высокого уровня вряд ли возможно, не имея хотя бы представлений о возможностях анализировать и эффективно управлять системами на базе решений, найденных с помощью факторного анализа.
Не следует обольщаться обещаниями популяризаторов факторного анализа, не следует верить мифам о его всемогущности и универсальности. Этот метод “на вершине” только по одному показателю — своей сложности, как по сущности, так и по сложности практической реализации даже при “повальном” использовании компьютерных программ.
Контрольные вопросы
1. Какие подходы Вы знаете к решению задач, в которых используются статистические данные?
2. Что показывает матрица ковариации и в каком анализе она используется?
3. Что показывает матрица корреляции и в каком анализе она используется?
4. В чем заключается идея метода компонентного анализа?
5. Когда имеет смысл проводить компонентный анализ?
6. Для чего служит факторный анализ?
7. В чем заключается идея метода факторного анализа?
Дата добавления: 2017-09-19; просмотров: 1988;
