Решение систем линейных и нелинейных алгебраических уравнений
С подобной задачей инженер сталкивается, пожалуй, чаще всего в своей практике. Уравнения, содержащие суммы целых степеней х, называются алгебраическими. К решению систем алгебраических уравнений приводят многие задачи анализа и синтеза физических явлений различной природы (механические, гидравлические, и т.д.). В теплоэнергетике к решению систем алгебраических уравнений приводят задачи: теплового и массового баланса процессов, гидравлического расчета тепловых сетей, систем теплоснабжения, анализа размерности при физическом моделировании и т.д.
В общем случае система линейных уравнений имеет вид:
a11 x1 + a22 x2 + . . . + a1n xn = b1
a21 x1 + a22 x2 + . . . + a2n xn = b2
. . . . . . . . . . . . . . . . . . . . . . . . . . ( 6.1 )
an1 x1 + an2 x2 + . . . + ann xn = bn
Систему (6.1) можно представить в векторно-матричной форме:
- матрица коэффициентов будет иметь вид
a11 a12 . . . a1n
a21 a22 . . . a2n
A = . . . . . . . . . . ;
an1 an2 . . . ann
- вектор -столбец свободных членов ( 6.2 )
b1
b2
b = …… ;
bn
- вектор-столбец неизвестных
x1
x2
x = ….. .
xn
Свернем (6.2):
Ax = b (6.3)
Если матрица А невырожденная, то есть ее определитель отличен от нуля, можно найти единственное решение системы (6.1) или (6.3) в виде:
xi=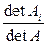 
, (6.4)
где в числителе определитель матрицы Ai.
Матрица Ai может быть получена из матрицы А, заменой ее i-го столбца, столбцом свободных членов. Такой метод решения мало эффективен, чаще всего используются численные методы решения, которые делятся на: прямые (точные) и итерационные (приближенные). К прямым относится метод Гаусса, к приближенным - метод Зейделя.
Распространенной вычислительной задачей является нахождение решений систем нелинейных алгебраических трансцендентных уравнений с n неизвестными, которые в общем виде можно записать так:
f1(x1,x2, . . . xn)=0
f2(x1,x2, . . . xn)=0
. . . . . . . . . . . . . . (6.5)
fn(x1,x2, . . . xn)=0
Решением такой системы называется множество значений x1,x2, . . . xn, одновременно удовлетворяющих каждому из уравнений системы.
Введем векторы столбцы:
x1 f1
x2 f2
x = . . . , f = . . . , тогда (6.5) преобразуется к виду
xn fn
f(x)=0. ( 6.6 )
Такие системы решаются только итерационными методами Ньютона и Зейделя.
Дата добавления: 2017-09-19; просмотров: 696;