Методы численного интегрирования

Формула прямоугольников

Впишем в каждую полоску прямоугольник. Для нахождения площади такого прямоугольника найдем координату средней точки х_ср = (x_i+x_i+1)/2 и значение функции в ней f (x_ср). Площадь под кривой определяется так

I=ΣI_i= Σf((x_i+x_i+1 )/2)*( x_i+1- x_i) (4.3).

Формула (4.3) - формула прямоугольников.

Оценим погрешность метода прямоугольников, для чего разложим функцию в ряд Тейлора и отбросим соответствующие члены ряда, содержащие h в степени больше 3.

Эта погрешность может быть определена так:

e_i = - (h³/24)* f ′′ (x_i),

ε = ∑ e_i = - (h²/24)* (b-a ) * f ′′ ( ξ ), (4.4).

где ξ є [ a , b ].

Метод трапеций

Впишем в каждую полоску трапецию. Площадь под кривой определяется так

I=ΣI_i= Σ1/2 (f (x_i+1)- f((x_i)) *( x_i+1- x_i) + f(x_i) *( x_i+1- x_i)

Формула трапеций на равномерной сетке шагом h =(x_i+1- x_i):

I = ∑ с_i * f (x_i) = h/2*( y₀ + 2y₁ + 2y₂ +... + y_n ) (4.5).

ⁱ

h = (b -а)/ n; у₀ = f (x₀); у₁ = f (x₁) и т.д.

Оценим погрешность метода трапеций, для чего разложим функцию в ряд Тейлора и отбросим соответствующие члены ряда, содержащие h в степени больше 3. Эта погрешность может быть определена так:

e_i = - (h³/12)* f ′′ (x_i)

ε = ∑ e_i = - (h²/12)* (b-a ) * f ′′ ( ξ ), где ξ є [ a , b ] (4.6).

4.2.3 Метод Симпсона

Этот метод аналогичен правилу трапеций в той части, где интегрирование производится путём разбиения общего интервала на множество более мелких отрезков. Однако теперь для вычисления площади каждой полоски через каждые три последовательные ординаты разбиения проводят квадратичную параболу.

Предположим, что число отрезков чётное:

n = (b-a) / h.

Воспользуемся методом трапеции:

I _h= h/2*( y₀ + 2y₁ + 2y₂ +... + y_n ) (4.7)

Площадь под кривой I = I _h+с h² (4.8)

Увеличим шаг в два раза k = 2h:

I _k= k/2*( y₀ + 2y₂ + 2y₄ +... + y_n ) (4.9)

Площадь под кривой I = I_k+с k². (4.10)

Исключив из системы уравнений (4.8) и (4.10) с, получим формулу Ричардсона для лучшего приближения интеграла

I = I _h+ (I _h - I_k)/ (k²/ h²-1) (4.11)

Подставим (4.7) и (4.9) в (4.11) получаем формулу Симпсона

I = h/3*( y₀ + 4y₁ + 2y₂ + 4y₃ + 2y₄ +... + y_n ) (4.12)

Ошибка ограничения, допускаемая в методе Симпсона

e_i = - (h⁴/180)* f ^(IV) (x_i)

ε = ∑ e_i = - (h⁴/180)* (b-a ) * f ^(IV) ( ξ ), (4.13)

где ξ є [a, b].

Метод трапеций и Симпсона наиболее часто используется при численном интегрировании.

Оценка погрешности ограничения рассмотренных методов численного интегрирования по выражениям (4.4), (4.6) и (4.13) оказываются малоэффективными из-за трудностей оценки производных высокого порядка подынтегральных функций. На практике для достижения требуемой точности прибегают к методу последовательного удвоения числа шагов. Задают значение допустимой погрешности ε и число интервалов разбиения n (шаг интегрирования h) находят I_n. Удваивают число интервалов (шаг интегрирования h/2) и находят I _2n. Оценивают погрешность Δ=( I_n- I _2n)/3 – для метода трапеций и Δ=( I_n- I _2n)/15 – для метода Симпсона. Если Δ≥ ε, количество интервалов еще раз удваивают. Вычисления заканчивают при выполнении условия Δ< ε.

4.2.4 Метод Гаусса

Гауссом предложен метод, позволяющий уменьшить ошибку ограничения при заданном числе интервалов за счет расположения концов интервалов там, где это требуется из условий достижения наивысшей точности интегрирования.

В заданном интеграле _b

I=ò f(x)dx,

^a

изменим пределы интегрирования так, чтобы они стали равны +1и –1, для чего введем новую переменную μ = (2х- (b+a))/(b-a)

₁

I=ò φ (μ)dμ, где φ (μ)=(1/2)(b-a) f((b-a) μ /2+(b+a)/2).

^-1

Можно показать, что

₁

I=ò φ (μ)dμ = φ (-1/√3) + φ (1/√3) +ε, (4.14)

^-1

где ε= φ ^(IV)/135.

(4.14)– формула Гаусса для двух ординат.

Можно вывести Гауссовы формулы численного интегрирования более высокого порядка с использованием полиномов Лежандра [1]. На практике предпочтение отдается методу Симпсона.

Интегрирование по квадратурным формулам сопровождается ошибками округления. Они носят случайный характер и с увеличением числа интервалов разбиения n возрастают пропорционально √n. Для функций высокой гладкости формула Гаусса дает значительно более точные результаты, чем формула Симпсона при одинаковом числе узлов, а последняя более точные, чем формула трапеций. Формула Гаусса обеспечивает высокую точность при небольшом числе узлов. Формула Симпсона в достаточной степени точна при умеренном числе узлов и поэтому получила широкое применение. Компьютерная реализация методов интегрирования описана в [9], [23-26].

Литература: [1-4],[6],[22-24].

Лекция 5

Тема: Численные методы нахождение корней алгебраических и трансцендентных уравнений

План: Нахождение корней алгебраических и трансцендентных уравнений при решении уравнений тепло - и массообмена. Методы нахождения корней уравнений: дихотомии, хорд, Ньютона, секущих, последовательных приближений.

5.1 Нахождение корней алгебраических и трансцендентных уравнений при решении задач тепло - и массообмена.

В научной и инженерской практике часто приходится решать алгебраические уравнения. Так при решении задачи нестационарной теплопроводности по определению температурного поля в бесконечной пластине толщиной 2δ было получено уравнение вида

Θ=Σ(2Θ₀sinμ_n/(μ_n+ sinμ_nсosμ_n)) сos(μ_nх/δ)exp(-μ_n²Fo),

в котором μ_n являлось корнем характеристического трансцендентного уравнения

μ_n/Bi=ctg μ_n.

Критериальные уравнения тепломассообмена, многие уравнения гидродинамики относятся к трансцендентным уравнениям [14-17].

Скорость и эффективность решений таких уравнений существенно влияют на применимость вычислительного процесса и определяются классом задачи. Алгебраические задачи могут быть классифицированы по числу уравнений, типу и количеству решений.

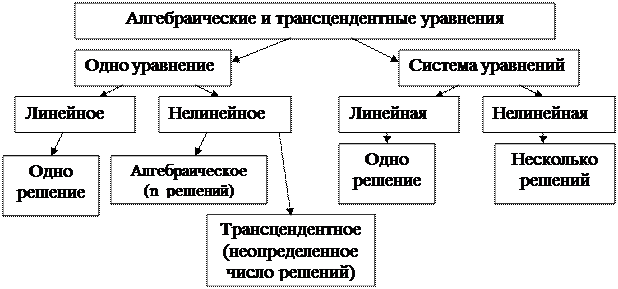
Рисунок 5.1 –Схема классификации алгебраических уравнений

Методы решения алгебраических уравнений делятся на прямые и итерационные.

Прямые это – например, нахождение корня квадратного уравнения.

В итерационных методах процедура решения задаётся в виде многократного применения некоторого алгоритма.

При решении таких задач предполагается, что корни являются действительными.

Отыскание корней уравнения состоит обычно из двух этапов. На первом этапе необходимо выяснить существуют ли решения, какого их количество, оценить примерное значение, оценить количество и величину интервалов, на котором функция меняет знак. Второй этап – нахождение корня в заданном интервале.

При решении задачи нахождения корней функции одной переменной вида f(x)=0, где f(x) – алгебраическая или трансцендентная функция, можно говорить только о приближенном вычислении корней уравнения, т. е. таких значений аргумента x=х^*, при которых выполняется равенство f(х^*)=0 с заданной точностью. Рассмотрим некоторые методы решения задач такого типа.