Численное интегрирование в теплотехнических расчетах

Необходимость численного интегрирования часто возникает при анализе инженерных и научных данных. Например, численные методы вычисления применяют в тех случаях, когда интеграл не удается найти в аналитическом виде или когда этот вид сложен. Численное интегрирование применяют и тогда, когда нужно найти интеграл от табулированной функции, измеряемой в эксперименте.

Например, для определения количества теплоты, передаваемого от одного теплоносителя к другому через поверхность теплообмена, необходимо воспользоваться уравнением теплопередачи вида

dQ = k<Dt>dF (4.1)

Из уравнения (4.1) t_x2

F=òdQ ¤ k<Dt> = òG_хc_рхdt_х ¤ k<Dt>(t_x,t_г )

t_x1

т.е задача сводится к взятию интеграла, что не всегда можно сделать аналитически.

Задача численного интегрирования состоит в нахождении приближенного значения интеграла вида:

,

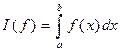где f(x) – заданная функция.

На отрезке [а,b] вводится сетка

ω ={x_i;; x₀ = а<x₁<x₂…<x_n = b}.

В качестве приближенного значения интеграла рассматривают число

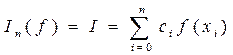, (4.2)

где f(x_i) – значения функции в узлах сетки;

с_i – весовые или квадратурные множители (веса), которые зависят только от узлов и не зависят от вида функции.

Формула (4.2) - квадратурная формула. Задача численного интегрирования будет состоять в отыскании таких узлов {x_i;} и таких весов {с_i;}, чтобы погрешность квадратурной формулы была минимальна для функций из заданного класса

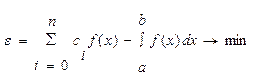
В зависимости от разбиения отрезка [а,b] различают два подхода к построению квадратурных формул. В первом - местоположение и длина интервалов разбиения выбираются заранее. В этом случае используется квадратурная формула Ньютона - Котеса (к этим методам относятся метод трапеции и метод Симпсона). Во втором - местоположение и длина интервалов заранее не задается, а подбирается так, чтобы достичь наивысшей точности при заданном числе интервалов (метод Гаусса).

Определенный интеграл

_b

I=ò f(x)dx (4.2)

^a

представляет собой площадь, ограниченную кривой f(x),осью х и прямыми х₀ = a, х _n= b. Мы будем пытаться вычислить интеграл, разбивая интервал от a до b на множество меньших интервалов, находя приблизительную площадь каждой полоски.

y f (x_i) f (x_i+1)

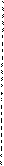
y = f (x)

a x_i x_i+1 b x

Рисунок 4.1 – Геометрическая интерпретация численного интегрирования