Интегрирование иррациональностей и тригонометрических выражений.
Иррациональности.
Если в подынтегральной функции присутствует корень какого-то порядка 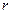 , то есть
, то есть 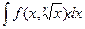 , то замена
, то замена 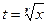 позволяет полностью избавиться от корней в выражении и свести к рациональной дроби.
позволяет полностью избавиться от корней в выражении и свести к рациональной дроби.
Из 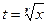 следует
следует 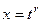 ,
, 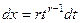 , то есть как видим, пересчёт дифференциала при замене тоже не добавляет ничего, кроме константы и целой степени от
, то есть как видим, пересчёт дифференциала при замене тоже не добавляет ничего, кроме константы и целой степени от 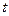 .
.
Рассмотрим сразу более общий случай: если функция содержит несколько корней разного порядка, т.е. 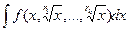 .
.
Тогда нужна замена на корень порядка r = НОК (r1,...,rk).
r это наименьшее общее кратное всех порядков, которые там есть.
Именно тогда все корни перейдут в целые степени от 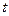 . Так, к примеру, если
. Так, к примеру, если 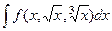 , то НОК = 6. Замена:
, то НОК = 6. Замена: 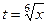 , тогда:
, тогда: 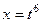 ,
,  . Каждый корень становится целой степенью от
. Каждый корень становится целой степенью от 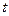 :
:
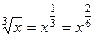 =
= 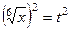 ,
,
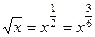 =
= 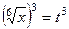 .
.
В общем случае степень равна 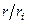 , то есть, какого множителя не хватает до наименьшего общего кратного, такая степень от
, то есть, какого множителя не хватает до наименьшего общего кратного, такая степень от 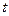 и получится.
и получится.
Рассмотрим на примере, содержащем 3 разных корня.
Пример Вычислить интеграл 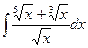 .
.
НОК (2,3,5) = 30. Поэтому замена 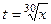 .
.
Тогда 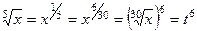 . Дополняющий множитель до НОК для числа 5 как раз и есть 6, ведь НОК = 30.
. Дополняющий множитель до НОК для числа 5 как раз и есть 6, ведь НОК = 30.
Другие корни пересчитываются аналогично:
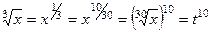 ,
,
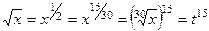 .
.
Надо ещё также пересчитать дифференциал для новой переменной 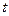 .
.
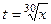
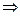
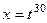
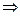
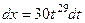 .
.
Теперь подставим всё это в интеграл.
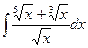 =
= 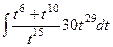 =
= 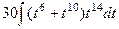 =
=
= 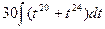 =
= 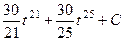 , и после обратной замены:
, и после обратной замены:
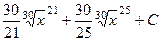 .
.
Если 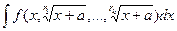 т.е. под корнем некоторое линейное выражение, то решается практически так же, замена
т.е. под корнем некоторое линейное выражение, то решается практически так же, замена 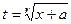 , где r это тоже наименьшее общее кратное. Более сложная ситуация, когда под корнем разные линейные функции.
, где r это тоже наименьшее общее кратное. Более сложная ситуация, когда под корнем разные линейные функции.
Например, 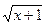 и
и 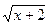 . Если один корень заменить на t ,
. Если один корень заменить на t , 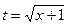 , то
, то 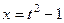 , тогда
, тогда 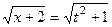 . Такие будут рассмотрены чуть позже в этом параграфе, они решаются с помощью тригонометрических функций.
. Такие будут рассмотрены чуть позже в этом параграфе, они решаются с помощью тригонометрических функций.
Если интеграл вида 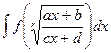 (где r - целое число), то замена
(где r - целое число), то замена 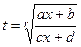 сводят всё к рациональной дроби от t.
сводят всё к рациональной дроби от t.
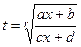
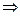
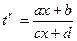
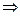
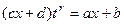
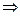
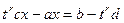
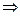
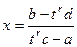 то есть
то есть 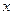 выражено в виде рациональной дроби от
выражено в виде рациональной дроби от 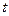 , содержащей только целые степени.
, содержащей только целые степени.
Дифференциал тоже выразится в виде рациональной дроби:
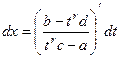 =
= 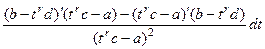 =
=
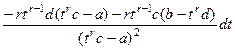 .
.
Дата добавления: 2017-05-18; просмотров: 527;
