Интегрирование дифференциального уравнения коллебаний.

При Р=0

Из решения видно что свободн. колеб-я явл-ся гармоничными (по з-ну Sin, Cos) с частотой w.

w – круговая частота свободных колеб-й

Свободные колебания в системе с 1-й степенью свободы.

В сис-ме с 1-й степ. Свободы свободные колеб-я всегда явл-ся собственными колебаниями с периодом и частотой, не зависящими от начальных условий движения, в то время как амплитуда и нач.фаза колебаний зависит от них.

Понятие о резонане

Резонанс-явление резкого возрастания амплитуды вынужденных колебаний в какой-либо колебательной системе, наступающее при приближении частоты периодического внешнего воздействия к некоторым значениям, определяемым свойствами самой системы

Явл-е резонанса возникает при 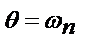,т.е при совпадении частоты возникающей силы с какой-либо из собственных частот системы.

Явл-е резонанса возникает только при 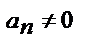т.е если наг-ка содержит состовляющую, пропорциональную кривой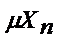

Если этой состовляющей нет резонанса не будет.

Если например наг-ка q(x;t) распределена по пролету семмитрично, а частота 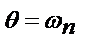явл-е резонанса не должно возникнуть, однако на практике не бывает абсолютно семмитрич-ой наг-ки или что коэфф-т аn сторого = 0

Харак-р явл-я резонанс зависит от св-в колебат-й сис-ы. Наиб. просто резонанс протекает в случаях,когда переодич-му возд-ию подвергается сис-ма с парам-ми не зависящ. от состо-я самой сист-мы.

Резонанс приводит в резкому увелич. амплитуды вынужд-х колеб-й всей констр-ии и может может привести к разруш-ю сооруж-я.

Для устранения его подбир-т св-ва системы так, чтобы нормал-е частоты были далеки от возмож-х частот внеш. возд-я, либо исп-ют явл-е антирезонанса (прим-ют поглатители колебан-й).