Интегрирование по частям

Интегрирование по частям производится по формуле:

,

Где u и v – функции переменной интегрирования, например х.

Пользуясь формулой интегрирования по частям, необходимо соблюдать требование, чтобы dx обязательно входило в состав dv и чтобы через dv была обозначена такая функция, интеграл которой можно легко найти.

Например,

.

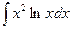Решение. Положим u=lnx, dv= x²dx, откуда (дифференцируя u и интегрируя dv)

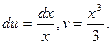
Постоянная С в этом случае не ставится; она будет поставлена в окончательном результате, когда будет найден данный интеграл.

Обращаемся теперь к формуле интегрирования по частям:

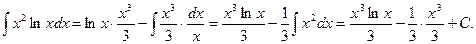
Определенный интеграл

Приращение F(b) – F(a) любой из первообразных функций F(x) + c при изменении аргумента от x = a до x = b называется определенным интегралом:

Геометрический смысл определенного интеграла выражает задача о площади криволинейной трапеции.

Алгоритм нахождения определенного интеграла

1 Найти первообразную функцию F (x) для функции ƒ(x).

2 Вычислить значение F (x) при x = b.

3 Вычислить значение F (x) при x = а.

4 Вычислить разность F(b) – F(a).