Основные формулы интегрирования

Интегрирование простейших функций

Одной из главных задач дифференционального исчисления является задача нахождение скорости изменения какой-либо функции, т.е. задача нахождения производной. На практике часто приходится решать обратную задачу: зная скорость изменения функции, найти эту функцию; эта задача называется интегрированием.

Функция F называетсяпервообразнойдля функции ƒ на некотором промежутке, если для всех x из этого промежутка существует производная F'(х), равная ƒ(х), т.е. F'(х)= ƒ(х).

Например. Найти первообразную для функции ƒ (х)= х³.

Решение.Функция F'(x)= x⁴⁄4есть первообразная для функции ƒ (х)= х³на промежутке (−∞;+∞), так как F' (х)=( x⁴ ⁄4 )' = ¼ ( х⁴ )' = ¼ × 4 х³ = х³.

Теорема 1.Если F(х) – первообразная для ƒ(х) на некотором промежутке, то сумма F(х)+с, где С= const, тоже является первообразной для ƒ (х) на этом промежутке,

(F(х)+с)'= (F(х))'+с' = ƒ (х)+ 0= ƒ (х)

Множество первообразных для данной функции ƒ(х) называется неопределённым интегралом и обозначается следующим образом:

∫ ƒ(х)dx = F(х)+С

ƒ(х) – подынтегральная функция,

ƒ(х)dx–подынтегральное выражение,

х- переменная интегрированная,

С- постоянная интегрированная,

F(х)-какая нибудь первообразная от функции ƒ(х).

Например, ∫ 2хdx = х²+ с

Операция нахождения неопределённого интеграла называется интегрированием функции.

Правила интегрирования

1) Для получения неопределённого интеграла от данной функции ƒ(х)необходимо найти одну из её первообразных и прибавить к ней произвольную постоянную.

2) Для проверки правильности полученного результата необходимо помнить, что производная от результата интегрирования должна равняться подынтегральной функции.

Основные свойства неопределённого интеграла

Свойство1. Производная от неопределённого интеграла равна подынтегральной функции, а дифференциал – подынтегральному выражению:

( ∫ ƒ(х)dx )' = ƒ(х) ; d ∫ ƒ(х)dx = ƒ(х)dx.

Свойство 2. Неопределённый интеграл от производной (дифференциала) функции равен этой функции, сложенной с произвольной постоянной:

∫ F'(х)dx = F'(х) + с или ∫ dF(x) =F(x)+ с.

Свойство 3. Постоянный множитель можно выносить за знак интеграла:

∫ af(x)dx = a∫ f(x)dx, где а = соnst, а ≠ 0.

Свойство 4. Неопределённый интеграл от алгебраической суммы двух или нескольких функций равен алгебраической сумме их интегралов:

∫ (ƒ(x)+y(x) –g(x))dx = ∫ ƒ(x)dx + ∫ y(x)dx – ∫ g(x )dx.

Основные формулы интегрирования

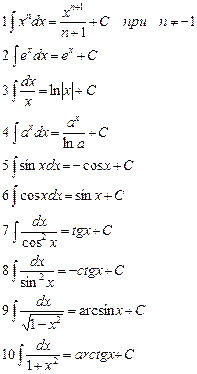
3. Вычисление определённых интегралов. Методы интегрирования

3.1. Непосредственное интегрирование