Интегрирование некоторых иррациональных выражений
1) Неопределенный интеграл вида 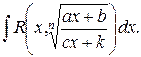
Подынтегральная функция – рациональная функция двух переменных 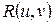 , где
, где 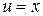 ,
, 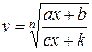 – иррациональная функция одной переменной
– иррациональная функция одной переменной 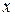 ,
, 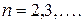
Теорема. Неопределенный интеграл 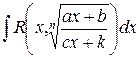 всегда может быть сведен к неопределенному интегралу от рациональной функции одной переменной
всегда может быть сведен к неопределенному интегралу от рациональной функции одной переменной 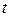 .
.
Сделаем замену переменной: 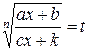 , то есть
, то есть 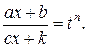 Отсюда находим:
Отсюда находим: 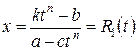 – рациональная функция переменной
– рациональная функция переменной 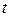 .
.
Найдем: 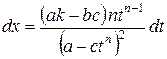 .
.
Функция 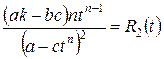 – рациональная функция переменной
– рациональная функция переменной 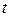 (предполагается, что
(предполагается, что 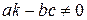 ),
), 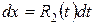
Таким образом,
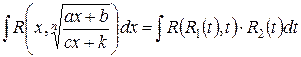 .
.
Подынтегральная функция 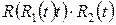 есть произведение двух рациональных функций одной переменной
есть произведение двух рациональных функций одной переменной 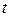 и является рациональной функцией
и является рациональной функцией 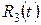 .
.
Итак, 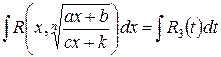 .
.
2) Неопределенный интеграл вида 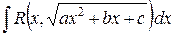
Подынтегральная функция – рациональная функция двух переменных 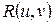 , где
, где 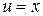 ,
, 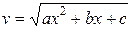 – иррациональная функция одной переменной
– иррациональная функция одной переменной 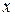 .
.
Теорема. Неопределенный интеграл 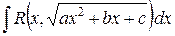 всегда может быть сведен к неопределенному интегралу от рациональной функции одной переменной
всегда может быть сведен к неопределенному интегралу от рациональной функции одной переменной 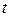 .
.
Если трехчлен 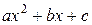 имеет действительные корни
имеет действительные корни 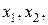
то 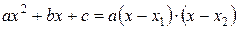 и
и
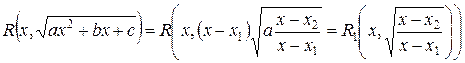 и интеграл сводится к случаю 1.
и интеграл сводится к случаю 1.
Поэтому будем считать, что 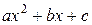 не имеет действительных корней и
не имеет действительных корней и 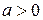 . Тогда рационализация интеграла может быть достигнута с помощью подстановки Эйлера:
. Тогда рационализация интеграла может быть достигнута с помощью подстановки Эйлера: 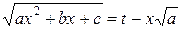 (эту подстановку можно применять и в случае действительных корней при
(эту подстановку можно применять и в случае действительных корней при 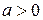 на интервале, где
на интервале, где 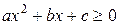 ). Отсюда
). Отсюда 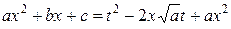 , то есть
, то есть 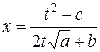 – рациональная функция от
– рациональная функция от 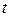 . Но тогда
. Но тогда 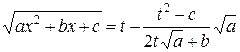 – также рациональная функция от
– также рациональная функция от 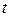 . Поэтому
. Поэтому 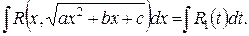
Замечание. Если 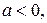 а
а 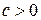 (
( 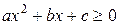 ), то можно сделать замену
), то можно сделать замену 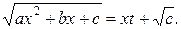
Пример. Вычислить 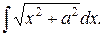
Бином 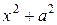 не имеет действительных корней. Поэтому полагаем
не имеет действительных корней. Поэтому полагаем 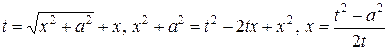 и
и 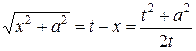
Отсюда 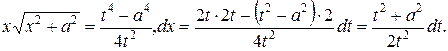
В силу этого
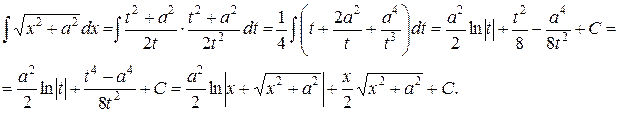
Неопределенный интеграл вида 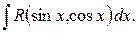
Теорема. Неопределенный интеграл вида 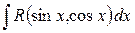 с помощью подстановки
с помощью подстановки 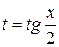
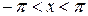 , которая называется универсальной, сводится к неопределенному интегралу от рациональной функции одной переменной
, которая называется универсальной, сводится к неопределенному интегралу от рациональной функции одной переменной 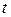 .
.
Сделаем подстановку
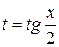 ,
, 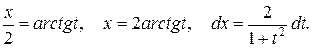
Выразим 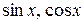 через
через 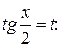
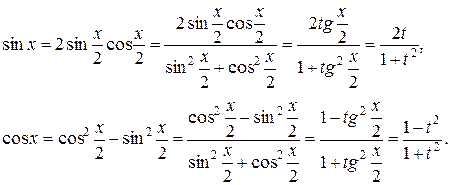
Тогда 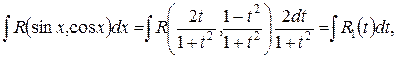 где
где 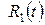 – рациональная функция от
– рациональная функция от 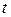 .
.
Пример. Вычислить 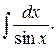
Сделаем подстановку 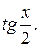
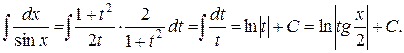
Несмотря на то, что универсальная подстановка дает возможность проинтегрировать всякую функцию вида 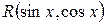 , однако на практике она часто приводит к слишком сложным рациональным функциям. Поэтому наряду с универсальной подстановкой полезно знать и другие подстановки, которые в некоторых случаях быстрее приводят к цели.
, однако на практике она часто приводит к слишком сложным рациональным функциям. Поэтому наряду с универсальной подстановкой полезно знать и другие подстановки, которые в некоторых случаях быстрее приводят к цели.
1) Если интеграл имеет вид 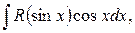 то подстановка
то подстановка 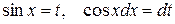 приводит этот интеграл к виду
приводит этот интеграл к виду 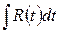 .
.
2) Если интеграл имеет вид 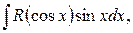 то он приводится к интегралу от рациональной функции заменой
то он приводится к интегралу от рациональной функции заменой 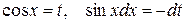 .
.
Пример. Вычислить 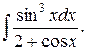
Сделаем замену 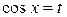 , тогда
, тогда 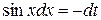 :
:
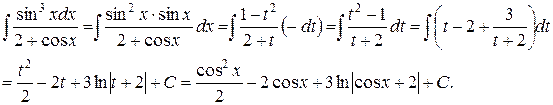
3) Если подынтегральная функция зависит только от 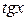 , то замена
, то замена 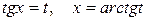 ,
, 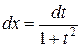 приводит этот интеграл к интегралу от рациональной функции:
приводит этот интеграл к интегралу от рациональной функции: 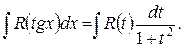
4) Если подынтегральная функция имеет вид 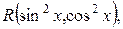 то применяется та же подстановка
то применяется та же подстановка 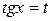 , так как
, так как 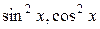 выражаются рационально через
выражаются рационально через 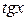 :
: 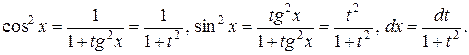
После подстановки мы получим интеграл от рациональной функции.
Пример. Вычислить 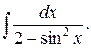
Сделаем замену 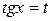 :
:
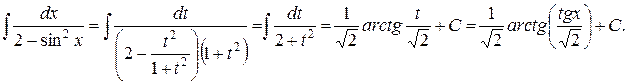
5) Рассмотрим интеграл вида 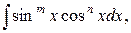 где
где 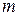 и
и 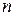 – целые числа. Здесь придется рассмотреть три случая.
– целые числа. Здесь придется рассмотреть три случая.
а) Если 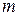 и
и 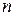 таковы, что по крайней мере одно из них нечетное, допустим для определенности, что
таковы, что по крайней мере одно из них нечетное, допустим для определенности, что 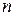 – нечетное.
– нечетное.
Положим 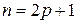 и преобразим интеграл:
и преобразим интеграл:
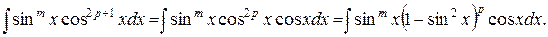
Сделаем замену 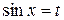 ,
, 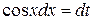 , получим интеграл от рациональной функции от
, получим интеграл от рациональной функции от 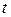 .
.
Пример. Вычислить 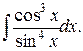
Обозначая 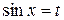 ,
, 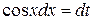 , получим:
, получим:
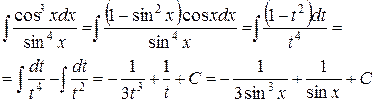
б) Если 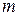 и
и 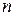 – числа неотрицательные и четные, то положив
– числа неотрицательные и четные, то положив 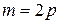 ,
, 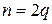 и применяя формулы, известные из тригонометрии
и применяя формулы, известные из тригонометрии
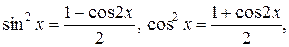 получим:
получим:
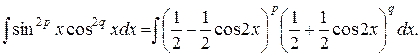
Возводя в степень и раскрывая скобки, получим члены, содержащие 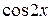 в нечетных и четных степенях.
в нечетных и четных степенях.
Члены с нечетными степенями интегрируются, как указано в случае а) Четные показатели снова понижаем по формуле 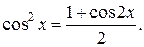 Продолжая так, дойдем до членов вида
Продолжая так, дойдем до членов вида 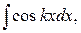 которые легко интегрируются.
которые легко интегрируются.
Пример. Вычислить 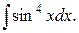
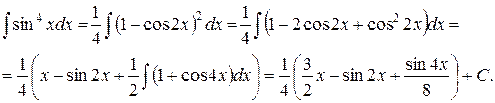
в) Если показатели 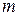 и
и 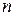 – четные, причем хотя бы один из них отрицателен, то следует сделать замену
– четные, причем хотя бы один из них отрицателен, то следует сделать замену 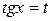 (случай 4)
(случай 4)
6) Рассмотрим интеграл вида
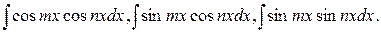
Он берется при помощи следующих формул 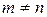 :
:
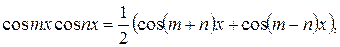
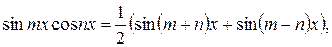
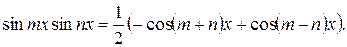
Пример. Вычислить 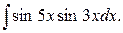
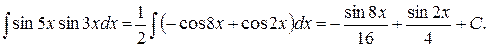
Дата добавления: 2019-07-26; просмотров: 496;
