Интегрирование по частям в неопределенном интеграле
Теорема. Если функции 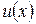 и
и 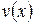 дифференцируемы в рассматриваемом промежутке, то
дифференцируемы в рассматриваемом промежутке, то 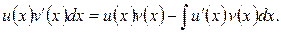
Так как 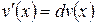 и
и 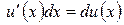 , то формулу интегрирования по частям можно представить в виде
, то формулу интегрирования по частям можно представить в виде 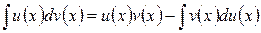 или краткой записи - формула интегрирования по частям:
или краткой записи - формула интегрирования по частям:
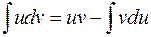 .
.
Обычно выражение 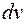 выбирается так, чтобы его интегрирование не вызывало особых трудностей. За
выбирается так, чтобы его интегрирование не вызывало особых трудностей. За 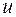 , как правило, принимается такая функция, дифференцирование которой приводит к ее упрощению. К классам функций, интегрируемых по частям, относятся, в частности, функции вида
, как правило, принимается такая функция, дифференцирование которой приводит к ее упрощению. К классам функций, интегрируемых по частям, относятся, в частности, функции вида 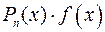 :
:
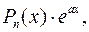
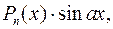
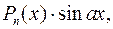
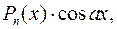
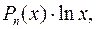
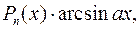
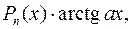 ,
,
где 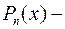 многочлен от
многочлен от 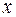 .
.
Указания
1. Правило выбора частей:
Если 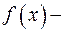 тригонометрическая или показательная функция, то следует положить
тригонометрическая или показательная функция, то следует положить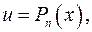
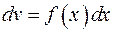 .
.
Если 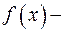 логарифмическая или обратная тригонометрическая функция, то
логарифмическая или обратная тригонометрическая функция, то 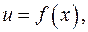
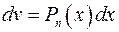 .
.
2. Интегрирование по частям можно применять несколько раз подряд.
3. Интегрирование по частям 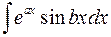 и некоторых других интегралов можно привести к линейному уравнению относительно этих интегралов после двукратного применения формулы интегрирования по частям.
и некоторых других интегралов можно привести к линейному уравнению относительно этих интегралов после двукратного применения формулы интегрирования по частям.
Примеры.
1) Рассмотрим неопределенный интеграл 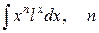 – натуральное число. В случае
– натуральное число. В случае 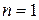 положим
положим 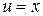 ,
, 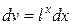 , тогда
, тогда 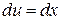 ,
, 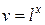 (произвольную постоянную опускаем) и
(произвольную постоянную опускаем) и
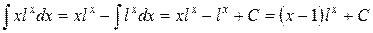 (1)
(1)
В случае 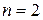 полагаем
полагаем 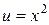 ,
, 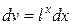 тогда,
тогда, 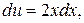
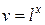 и
и
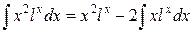 (2)
(2)
Из равенств (1) и (2) следует, что
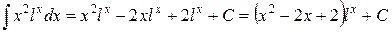 (3)
(3)
В случае 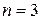 полагаем
полагаем 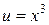 ,
, 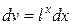 тогда
тогда 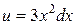 ,
, 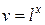 и
и
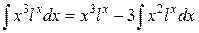 (4)
(4)
Из равенств (3) и (4) следует, что 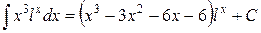 .
.
Аналогично можно поступить при 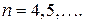
2) Аналогично можно найти 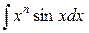 и
и 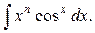
Например, рассмотрим, 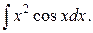 Положив
Положив 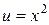 ,
, 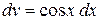 ,найдем
,найдем 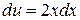 d и
d и 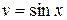 . То есть
. То есть 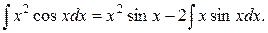
Положим теперь 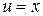 ,
, 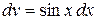 . Следовательно,
. Следовательно, 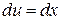 и
и 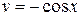 . Так что
. Так что 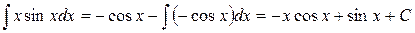 и потому
и потому
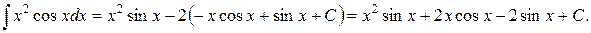 3) Рассмотрим неопределенный интеграл вида
3) Рассмотрим неопределенный интеграл вида 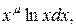 положим
положим 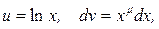 тогда
тогда 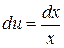 и
и 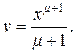
Имеем:
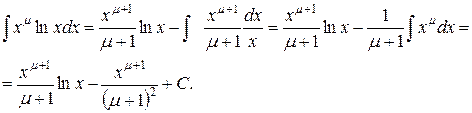
Итак, 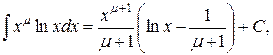
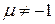 . В частности, для
. В частности, для 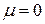 :
: 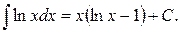
4) Рассмотрим неопределенный интеграл 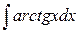 .
.
Положим 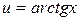 ,
, 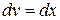 , тогда
, тогда 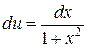 и
и 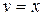 .
.
Имеем 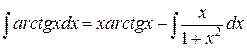 . Но
. Но
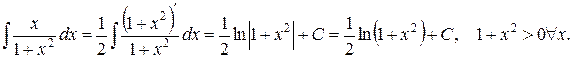
Итак, 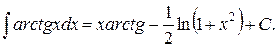
5) Рассмотрим неопределенный интеграл 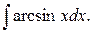
Положим 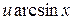 ,
, 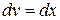 , тогда
, тогда 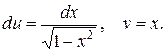
Имеем 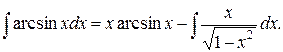 Сделаем замену переменной:
Сделаем замену переменной: 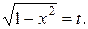 Тогда
Тогда 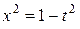 и
и 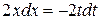 .
.
Значит, 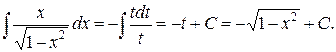
Следовательно, 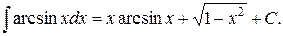
Дата добавления: 2019-07-26; просмотров: 407;
