Интегрирование по частям

Пусть u = u(x) и v = v(x) – дифференцируемые функции. По свойству дифференциала

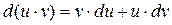или

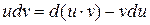
Интегрируя левую и правую части последнего равенства, получим:

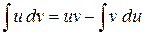(1)

(1) – формула интегрирования по частям.

Примеры:

1.

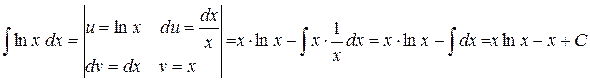
2.

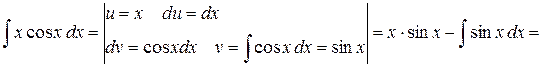
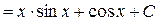
Если принять ,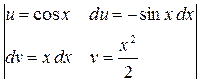

то 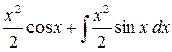– интеграл получился еще более сложным.

3.

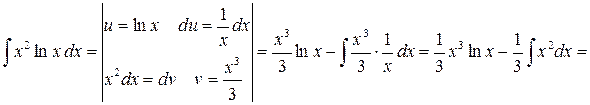
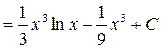
Проверка:

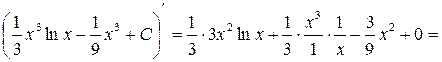
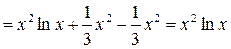
4.

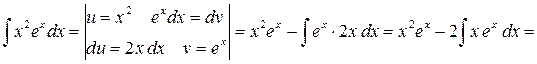
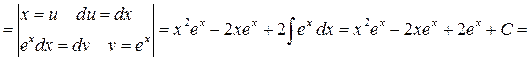
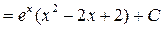
Замечание:

Нет определнных указаний на то, какое выражение брать в качестве u, а какое в качестве v.

Большую часть интегралов можно разбить на 3 группы:

1.

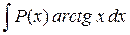
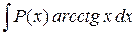
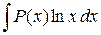
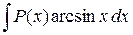
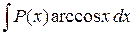
где P(x) – многочлен от х

Обычно помогают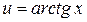

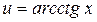
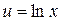
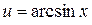
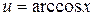
а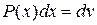

2.

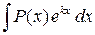
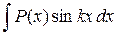
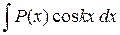
где P(x) – многочлен от х, k – некоторое число.

следует положить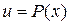

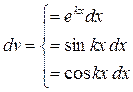
3.

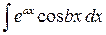
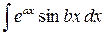
где a и b – некоторые числа

Эти интегралы вычисляются двукратным интегрированием по частям

Пример:

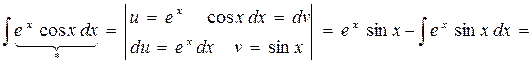
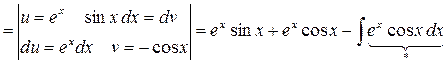
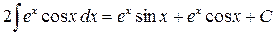
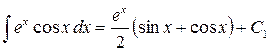
где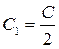

Лекция 5. МАТРИЦЫ И ОПЕРАЦИИ НАД НИМИ

Вопросы:

1. Основные сведения о матрицах.

2. Виды матриц.

3. Операции над матрицами.

4. Свойства операций над матрицами

5. Определители и способы их вычисления.

6. Свойства определителей.

7. Общие понятия СЛУ.

8. Методы решения СЛУ.