Основные сведения о матрицах

Матричная алгебра имеет важное значение для экономистов, так как значительная часть математических моделей экономических объектов и процессов записывается в простой и компактной форме числовых таблиц.

Опр.: Матрицей называется прямоугольная таблица чисел.

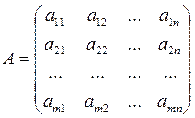Пример: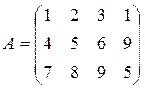

m – количество строк, n – количество столбцов.

Размерность матрицы m х n.

Обозначения: А; А(a_ij)

a_ij – элемент матрицы А, расположенный на i-той строке, в j-том столбце.

Мы рассматриваем только 1 и 2-мерные матрицы. В сложных структурах возможны матрицы любых размеров.

Виды матриц

1. Матрицы размерности 1 х n

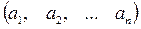– матрица-строка.

2. Матрица размерности m х 1

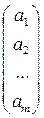– матрица столбец.

3. Опр.: Матрицы А = (a_ij) и B = (b_ij) 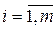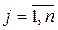называются равными
A = B, если 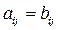∀ i, j.

4. Опр.: Если количество строк в матрице равно количеству столбцов, то матрица называется квадратной.

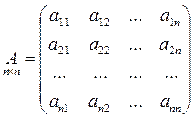Пример: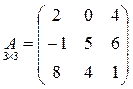

Элементы a_ij образуют главную диагональ матрицы.

5. Опр.: Если в матрице все элементы, кроме диагональных равны 0, то матрица называется диагональной.

Пример: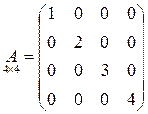

Если 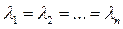– матрица скалярная.

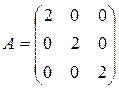
6. Если в диагональной матрице все диагональные элементы равны 1, то матрица называется единичной.

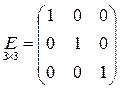
7. Если все элементы матрицы равны 0, то матрица называется нулевой или нуль-матрицей.

8. Треугольная или матрица ступенчатого вида – если все элементы над или под главной диагональю равны нулю:

;

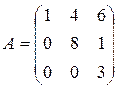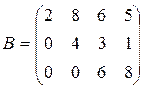
9. Симметричная матрица, если a_ij = a_ji

10. Противоположная (не путать с обратной) A = (a_ij) –A = (–a_ij)

11. Кососимметричная a_ik = –a_ki, a_ii = 0.