Свойства определителей
1. Определитель не изменится при замене строк столбцами, т.е. транспонировании 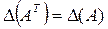
2. При перестановке двух строк (столбцов) матрицы ее определитель меняет знак на противоположный
3. Если все элементы строки (или столбца) матрицы умножить на число λ, то и определитель тоже умножится на λ.
4. Если квадратная матрица содержит две одинаковых строки или столбца, то ее определитель = 0.
Доказательство: Действительно, с одной стороны, если мы поменяем местами одинаковые строки (столбцы), то Δ не изменится, т.к. не изменится матрица, но по свойству (2) определитель меняет знак, т.е. Δ = –Δ ⇒ Δ = 0.
5. Если элементы двух строк или столбцов матрицы пропорциональны, то ее Δ = 0.
6. Если матрица содержит нулевую строку или столбец, то ее Δ = 0.
7. Определитель матрицы не изменяется, если к элементам какой-либо строки (столбца) матрицы прибавить элементы другой строки (столбца), уменьшенные на одно и то же число.
8.Если элементы какой-либо строки (столбца) определителя представляют собой сумму двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей.
9. Определитель произведения матриц равен произведению определителей этих матриц:
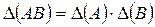
Общие понятия СЛУ
Опр.: Система m линейных уравнений с n неизвестными имеет вид:
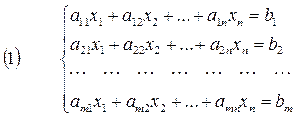
где aij, bi – произвольные числа;
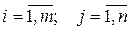 ;
;
aij – коэффициенты при неизвестных;
bi – свободные элементы;
i – номер уравнения;
j – номер неизвестного.
В матричном виде: 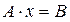 , где
, где
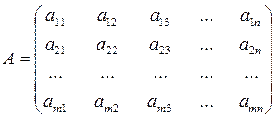 – матрица системы.
– матрица системы.
 – столбец неизвестных.
– столбец неизвестных. 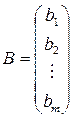 – столбец свободных элементов.
– столбец свободных элементов.
Опр.: Решением СЛУ (1) называется набор (массив) n чисел 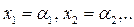
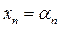 , при подстановке которых в эту систему каждое уравнение этой системы превращается в тождество.
, при подстановке которых в эту систему каждое уравнение этой системы превращается в тождество.
Опр.: СЛУ (1) называется совместной, если она имеет хотя бы одно решение; если система не имеет решений, она называется несовместной.
Совместная система имеет либо 1 решение и в таком случае она называется определенной, либо, если у нее больше 1 решения, она неопределенной.
Опр.: СЛУ вида (1) называется эквивалентными, если они имеют одно и то же множество решений.
Элементарные преобразования исходной системы приводит к эквивалентной системе.
Опр.: Матрица 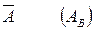
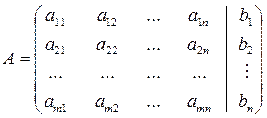
размерность m х (n+1) называется расширенной матрицей системы.
Теорема Кронекера-Канелли:
СЛУ совместна ⇔ когда ранг матрицы системы равен рангу расширенной матрицы системы.
Методы решения СЛУ
Матричный метод
Пусть m = n, тогда А – квадратная
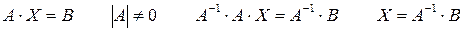
Пример:
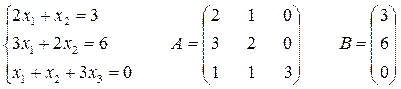
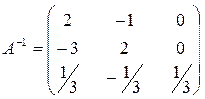 см. лекцию об обратной матрице.
см. лекцию об обратной матрице.
Тогда 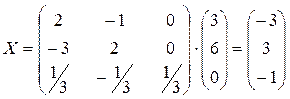
Ответ: 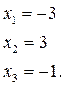
Метод Крамера
Опр.: Определитель 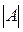 матрицы СЛУ называется определителем СЛУ и обозначается Δ.
матрицы СЛУ называется определителем СЛУ и обозначается Δ.
Заменим в этом определителе j-тый столбец на столбец свободных элементов В, получим другой определитель (обозначается Δj или Δxj).
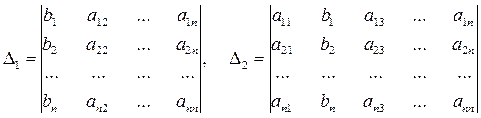 и т.д.
и т.д.
Теорема Крамера: Пусть Δ – определитель матрицы А СЛУ, Δj – определитель матрицы полученной из определителя Δ заменой j-того столбца на столбец B. Тогда, если Δ ≠ 0, то СЛУ имеет единственное решение:
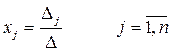
! Д/з: Доказательство самостоятельно (учебник Крамера, Красса).
Пример:
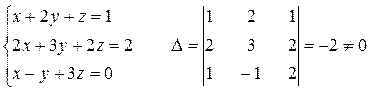
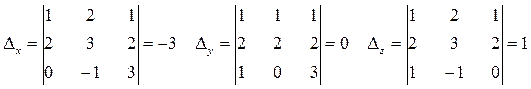
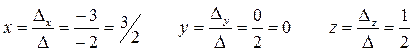
3. Метод Гаусса – метод последовательного исключения переменных
Рассмотрим на примере:
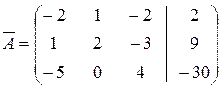 – расширенная матрица системы.
– расширенная матрица системы.
Приведем ее к ступенчатому виду:
Прямой ход:






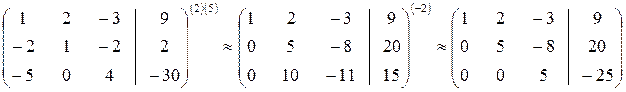 Обратный ход:
Обратный ход:
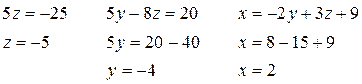
Ответ: (2; –4; –5)
! Д/з: Проверка самостоятельно.
Возможна ситуация:
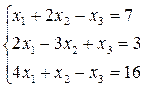




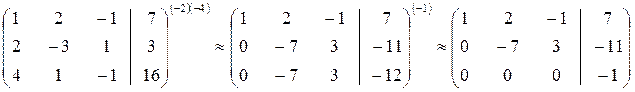 Уравнение, соответствующее 3-й строке, противоречиво, приводит к неверному равенству 0 = –1. Это означает, что данная СЛУ – несовместная.
Уравнение, соответствующее 3-й строке, противоречиво, приводит к неверному равенству 0 = –1. Это означает, что данная СЛУ – несовместная.
Дата добавления: 2017-09-19; просмотров: 528;
