Первообразная функции

Основной задачей дифференциального исчисления является нахождение производной или дифференциала данной функции.

Интегральное счисление решает обратную задачу – нахождение самой функции по ее производной или дифференциалу.

Опр.: Функция 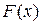называется первообразной функцией для функции 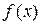на промежутке Х, если в каждой точке х этого промежутка

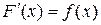
Например:

1) 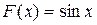является первообразной для функции 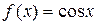, т.к.

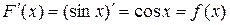
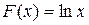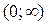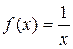2. на промежутке для , т.е.

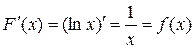
Исходя из геометрического смысла производной: 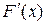– угловой коэффициент касательной к кривой 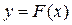в точке х

Значит, найти первообразную для 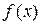– найти такую кривую 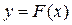, что угловой коэффициент касательной к ней в произвольной точке х равен значению 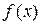заданной функции в этой точке

Следует заметить, что для заданной функции 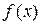ее первообразная определена неоднозначно.

Например:

Функции 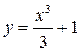, 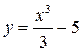и вообще функции 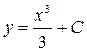, где С – некоторое действительное число, являются первообразными для функции

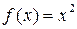
В общем случае, если 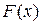– некоторая первообразная для 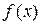, то поскольку

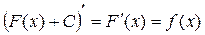
функции вида 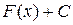, где С – произвольное число так же являются первообразными для .

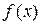Геометрически это означает, что если найдена одна кривая 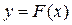, удовлетворяющая условию 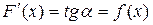, то сдвигая ее вдоль оси Оу, мы вновь получаем кривые, удовлетворяющие указанному условию (поскольку такой сдвиг не меняет углового коэффициента касательной).

Опр.: Совокупность всех первообразных для функции 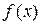на промежутке Х называется неопределенным интегралом от функции .

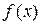Обозначение: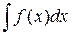

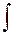– знак интеграла

х – переменная интегрирования

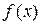– подинтегральная функция

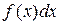– подинтегральное выражение

Пример:

1)

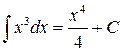
2)

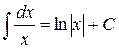
Операция нахождения неопределенного интеграла от некоторой функции называется интегрирование функции (обратная к операции дифференцирования).