Умножение матрицы на число

Любую матрицу можно умножить на любое число. Для этого каждый элемент матрицы умножается на это число:

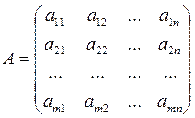
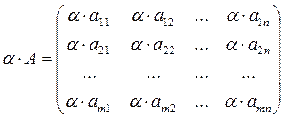
Пример: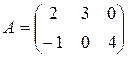

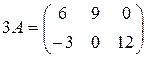
Следствие: Можно выносить общий множитель из-под матрицы:

Пример: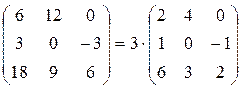

2. Сложение (вычитание) матриц:

Любые две матрицы одних и тех же размерностей! можно сложить (вычесть. Для этого их элементы с одинаковыми индексами складываются (вычитаются.

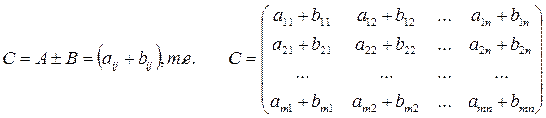
Пример: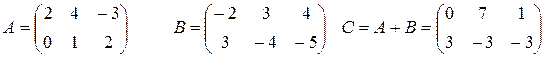

3. Умножение матриц:

Иногда (не всегда!!!) матрицы можно умножить одну на другую.

Эти операции можно выполнить только в том случае, если количество столбцов 1-го множителя равно количеству строк 2-го множителя, т.е. 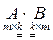, при этом полученная матрица будет иметь размерность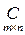

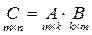
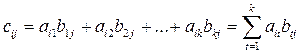
т.о. с₁₁ равен сумме произведений элементов 1-й строки матрицы А на элементы первого столбца матрицы В.

Пример: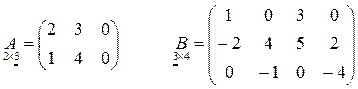

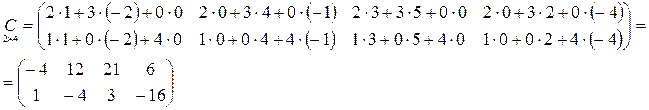
Как видно, для матриц не всегда выполняется закон АВ = ВА.

Если это равенство выполняется, то матрицы А и В называются коммутативными.

а) скалярная матрица коммутирует с ∀ квадратной матрицей того же порядка;

б) коммутативны диагональные матрицы одного порядка;

в) AF = FA = A.

Деление матриц

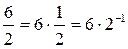аналогично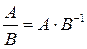

В^-1 – рассмотрим далее.