Преобразования подынтегральных выражений.
Различные преобразования, например, арифметические (домножить и поделить, прибавить и отнять), выделение полного квадрата, разбиение многочлена на множители, преобразования по тригонометрическим формулам, и т.д. нередко помогают упростить исходное выражение, разбить его на несколько более простых слагаемых, которые уже сводятся к интегралам табличного типа. На практике рассмотрены разнообразные примеры на виды этих преобразований. Часто нужно домножить и поделить, чтобы сформировать готовое выражение, являющееся производной от известной функции. Например,
Пример. 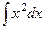 =
= 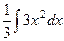 =
= 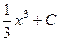 .
.
Когда сформировали выражение 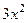 , а заодно поделили на 3 перед интегралом, теперь уже точно невозможно перепутать или забыть коэффициент.
, а заодно поделили на 3 перед интегралом, теперь уже точно невозможно перепутать или забыть коэффициент.
Аналогично, допустим, что мы помним, что 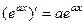 . Тогда можно постараться сформировать готовое выражение типа
. Тогда можно постараться сформировать готовое выражение типа 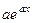 внутри интеграла. Тем самым мы автоматически докажем, что при интегрировании такое выражение на этот коэффициент делится, а не домножается:
внутри интеграла. Тем самым мы автоматически докажем, что при интегрировании такое выражение на этот коэффициент делится, а не домножается:
Пример. 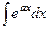 =
=  =
= 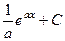 .
.
Тригонометрические преобразования:
Пример. Вычислить 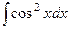 .
.
Решение. Применим формулу понижения степени.
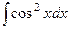 =
= 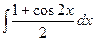 =
= 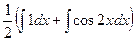 =
=
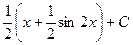 =
= 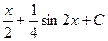 .
.
Пример. Вычислить 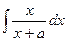 .
.
Решение. 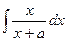 =
= 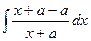 =
= 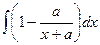 =
=
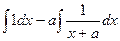 =
= 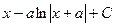 .
.
Ответ. 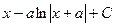 .
.
Замена переменной.
Бывают такие случаи, когда функция имеет вид 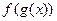 , то есть явно видно, что всё выражение зависит от какого-то однотипного блока, например всё выражается через
, то есть явно видно, что всё выражение зависит от какого-то однотипного блока, например всё выражается через 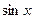 или
или  . Делается замена на
. Делается замена на 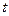 , только нужно не забыть пересчитать
, только нужно не забыть пересчитать 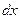 , потому что
, потому что 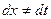 , если только замена не является простым линейным сдвигом
, если только замена не является простым линейным сдвигом 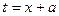 .
.
Пример. Вычислить 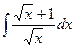 .
.
Решение. Сделаем замену 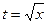 , тогда
, тогда 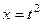 ,
, 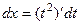 ,
, 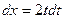 .
.
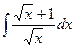 =
= 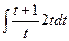 =
= 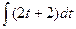 =
= 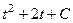 .
.
Обратная замена: 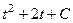 =
= 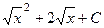 =
= 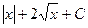 .
.
Более того, область определения исходной функции 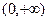 из-за наличия в ней квадратного корня, точка 0 не входит в область определения, так как корень там и в знаменателе, так что знак модуля в ответе является излишним, ответ можно записать так:
из-за наличия в ней квадратного корня, точка 0 не входит в область определения, так как корень там и в знаменателе, так что знак модуля в ответе является излишним, ответ можно записать так: 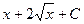 .
.
Если в функции присутствуют корни разного порядка, например  и
и 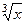 , то замена должна происходить через корень порядка НОК (наименьшее общее кратное). Причина в том, что именно при этом все корни переводятся в целые степени от
, то замена должна происходить через корень порядка НОК (наименьшее общее кратное). Причина в том, что именно при этом все корни переводятся в целые степени от 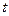 .
.
Если 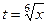 , тогда:
, тогда: 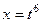 ,
,  .
.
Объяснение, почему все корни выразятся через целые степени 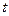 :
:
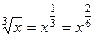 =
= 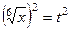 ,
,
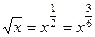 =
= 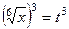 .
.
Дата добавления: 2017-05-18; просмотров: 793;
