Методы интегрирования.

Определения и основные методы.

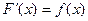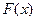Определение. Если , то называется первообразной от функции .

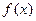Свойство.Если 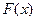первообразная, то 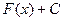(для любого 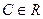) тоже является первообразной для той же самой функции .

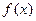Это легко доказать, действительно, = = .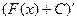

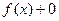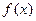Таким образом, первообразных бесконечно много, то есть, если поднять или опустить на любую высоту график 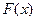, снова будет первообразная.

Свойство.Есл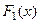и и 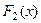две различные первообразные функции 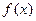, то .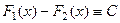

Доказывается так: 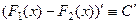, то есть .

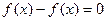Определение. Множество всех первообразных от одной и той же функции 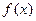называется неопределённым интегралом этой функции.

Обозначение: .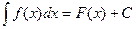

Свойства линейности.

1.

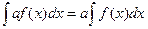
2.

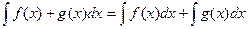
Замечание.

Для произведения свойство 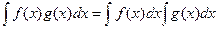не существует. Чтобы убедиться в этом, достаточно рассмотреть любые 2 простейшие функции, например 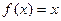, 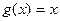. Тогда:

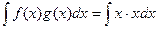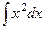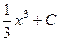= = , в то же время

= = .

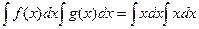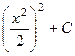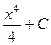Впрочем, можно даже рассмотреть 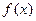произвольную, 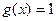. Тогда ,

= .

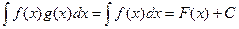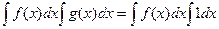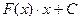Таблица основных интегралов.

( )

;

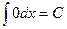
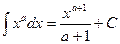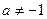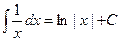
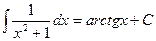
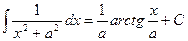
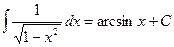
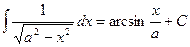
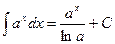
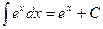
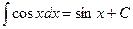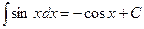
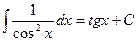
Объяснение причины возникновения модуля в 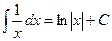. Функция 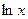существует только на правой полуоси, тогда как 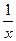имеет две ветви, на правой и левой полуоси. Получалось бы противоречие, что производная от несуществующей функции есть на левой полуоси. Функция 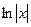является чётным продолжением 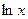на левую полуось, и именно она там является первообразной для 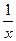при .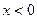

Методы интегрирования.