Компьютерные технологии в моделировании теплоэнергетических систем, процессов и установок. Модели и виды моделирования.
План: Введение. Цели и задачи курса. Политика курса. Состояние и перспективы использования компьютерных технологий в моделировании теплоэнергетических систем, процессов и установок. Классификация моделей и видов моделирования.
Курс «Компьютерные технологии в теплоэнергетических расчетах» является дисциплиной по выбору для студентов бакалавриата и включен в учебные планы в качестве базовой дисциплины.
Цель курса – формирование знаний, умений и навыков применения компьютерных технологий для расчета объектов теплоэнергетики и теплотехнологии.
Задачи курса: овладение элементами численных методов; приемами алгоритмизации; закрепление навыков, приобретенных в курсе «Информатика», использования языков программирования; проведение вычислительного эксперимента; использование компьютерных технологий и пакетов прикладных программ для исследования процессов, установок и систем теплоэнергетики и теплотехнологии.
Политика курса дана в силлабусе.
Дисциплина «Компьютерные технологии в теплоэнергетических расчетах» базируется на знаниях и умениях, приобретенных студентами при изучении курсов «Математика», «Информатика», «Физика», «Химия», «Материаловедение», «Техническая термодинамика», «Механика жидкости и газа», «Тепломассообмен». Знания, умения и навыки, полученные студентами, используются при изучении специальных дисциплин, в частности, курса «Методы моделирования и оптимизации теплоэнергетических и теплотехнологических процессов и установок», выполнении курсовых, дипломной и научно-исследовательских работ.
В результате изучения дисциплины бакалавры должны:
- иметь представлениео возможностях компьютерных технологий при решении прикладных задач теплоэнергетики и теплотехники;
- владеть:
- способами алгоритмизации и программирования, хранения, обработки и представления информации;
- методами:
- интерполирования функций;
- численного интегрирования;
- решения трансцендентных уравнений, систем алгебраических уравнений, обыкновенных дифференциальных уравнений;
- решения задач оптимизации;
- решения задач стационарной и нестационарной теплопроводности, конвективного теплообмена и т.д.;
- уметь:
- выбирать эффективный численный метод для решения конкретной задачи, оценивать его точность и надежность;
- использовать:
- языки высокого уровня для составления программ расчета;
- текстовые и графические редакторы, мультимедийные средства и компьютерную сеть;
- готовые пакеты прикладных программ для выполнения теплоэнергетических расчетов;
- автоматизированные экзаменационно – обучающие компьютерные системы для самообучения и самоконтроля;
- разрабатывать и использовать информационно-справочные системы и базы данных для обеспечения моделирования теплоэнергетических объектов.
- быть компетентным в выборе:
- численных методов и их программного обеспечения для решения профессиональных задач;
- средств их компьютерной реализации.
Для современного этапа развития теплоэнергетики характерны две тенденции. Первая - увеличение разнообразия условий функционирования теплоэнергетических установок, вызванное расширением диапазона видов, качества и стоимости сжигаемого топлива, типов применяемых систем охлаждения и режимов использования. Вторая – увеличение числа типов и модификаций, используемых и разрабатываемых теплоэнергетических установок, что связано с развитием атомных энергоустановок различных типов, созданием высокоманевренных модификаций паротурбинных, газотурбинных и парогазовых установок.
Эти тенденции приводят к возрастанию значимости технико-экономических исследований по определению оптимальных значений параметров, рационального вида технологической схемы и профилей оборудования энергоустановок различных типов. В настоящее время решение таких задач немыслимо без широкого использования компьютерных технологий и методов моделирования.
Специалист в области теплоэнергетики должен иметь достаточную подготовку в области информационных технологий - использовать программные средства общего пользования: Microsoft Office, Corel Draw, Adobe Photoshop и т.д., специализированные программные средства: AutoCAD, MathCAD, Mathlab, уметь работать в сети, с электронной почтой, в Интернете, знать языки высокого уровня, составлять алгоритмы и программы для решения профессиональных задач.
Трудно назвать отрасль знаний, указать сферы человеческой деятельности, где бы ни применялись и куда бы ни внедрялись в настоящее время методы моделирования.
Использование методов моделирования обусловлено:
- общей тенденцией расширения и углубления исследования процессов в реальном физическом мире;
- длительностью ряда процессов (например, экологических);
- практической невозможностью получать необходимую информацию путем исследования объекта-оригинала (микро- и макрообъекты);
- неполнотой данных о реальных процессах и высокой стоимостью исследований объекта-оригинала, когда с экономических позиций наиболее приемлемо перенести их на объект-модель;
- наличием критических режимов функционирования объекта, когда исследования в некоторых областях изменения экзогенных параметров являются попросту опасными, а результаты исследования не поддаются прогнозу;
- отсутствием условий, а иногда и недостаточной квалификацией персонала для исследования объекта-оригинала;
- необходимостью большого числа экспериментов;
- уникальностью объекта исследования;
- отсутствием объекта-оригинала и т.д.
Моделирование – метод исследования объектов познания на их моделях; построение и изучение моделей реально существующих предметов и явлений (инженерных устройств, физико-химических процессов) и конструируемых объектов для определения либо улучшения их характеристик, рационализации способов их построения, управления ими и т.п.
Модель – аналог (схема, структура, знаковая система) определенного фрагмента природной или социальной реальности – оригинала модели. Такой аналог служит для: хранения и расширения знаний об оригинале, конструирования оригинала, преобразования или управления им.
Формы моделирования разнообразны и зависят от используемых моделей и сферы применения моделирования.
Предметным называется моделирование, в ходе которого исследование ведется на модели, воспроизводящей определенные геометрические, физические, динамические либо функциональные характеристики объекта моделирования – оригинала. К предметному относится аналоговое моделирование, когда оригинал и модель описываются едиными математическими соотношениями.
При знаковом моделировании моделями служат чертежи, схемы, формулы.
Важнейшим видом знакового моделирования является математическое моделирование.
Моделирование применяется вместе с другими общенаучными методами исследования: экспериментом, абстрагированием, идеализацией и т.д.
Модели и виды моделирования можно разделить на три группы:
- первая – определяется характером функционирования объекта;
- вторая – средствами моделирования;
- третья (относится к математическим моделям) – типом математического описания.
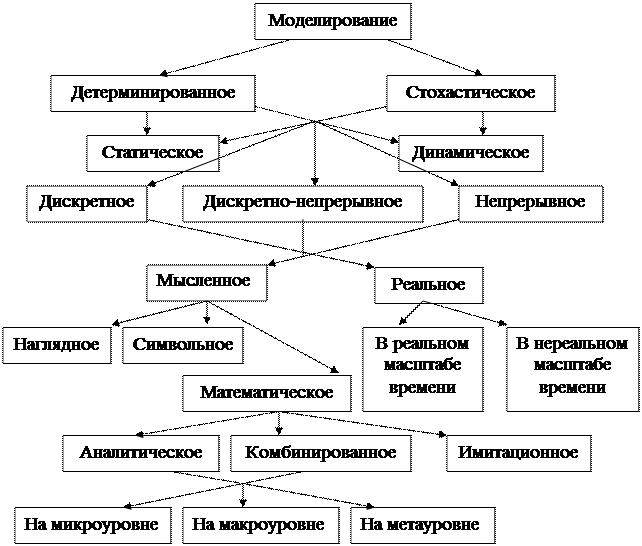
Рисунок 1.1 - Классификация видов моделирования
Поскольку все процессы могут протекать при наличии или отсутствии случайных воздействий, их моделирование носит детерминированный или стохастическийхарактер. Динамическое илистатическое моделирование определяется стационарностью и нестационарностью процессов в исследуемом объекте. Периодичность функционирования объекта-оригинала отражается дискретным, дискретно-непрерывными непрерывныммоделированием.
Наглядное моделирование связано с описанием модели на основе представлений, гипотез, выдвигаемых человеком, и применения аналогий различных уровней.
Символьное моделирование отображает свойства объекта-оригинала определенной заранее отработанной системой символов.
Модели на микроуровне обычно формализуют объекты с распределенными параметрами и описываются системами дифференциальных уравнений в частных производных.
Модели на макроуровне обычно представляются обыкновенными дифференциальными уравнениями (задача Коши и краевая задача) и алгебраическими уравнениями. Они используются для моделирования процессов с сосредоточенными параметрами в стационарной и нестационарной постановках.
Модели на метауровне создаются для сложных технических объектов и используются в основном при моделировании систем массового обслуживания и систем автоматического управления.
Имитационное моделирование заключается в создании модели-имитатора работы сложных (чаще при наличии стохастических факторов) систем и процессов при неполных знаниях о ряде процессов в моделируемых объектах. Они не позволяют в отличие от аналитических моделей формировать решение в обычном виде, но за счет перебора вариантов позволяют выбрать приемлемое решение.
Комбинированное моделирование состоит из аналитического моделирования, включая элементы имитационного моделирования, и наоборот.
Реальное моделирование представляет разработку физических полноразмерных или масштабных моделей агрегатов (процессов).
В 2007г. кафедрами ТЭУ и ПТЭ приобретен программный продукт МЭИ «ТВТ Shell» и материалы Электронной Энциклопедии Энергетики.
Электронная Энциклопедия Энергетики включает следующие разделы: общие вопросы теплоэнергетики; теоретические основы теплотехники; тепломеханическое оборудование ТЭС; теплообменное оборудование ТЭС; водоподготовка; водно-химический режим; КИП и автоматика; энергосбережение, экология и охрана труда; топливоиспользование и технология масел; эксплуатация оборудования; тепловые сети. Кроме того, энциклопедия содержит виртуальные лабораторные работы, программы тестирования и тренажеры.
Достаточно большое количество материалов по применению компьютерных технологий в теплоэнергетике и теплотехнике представлено в настоящее время в Интернете. Это – интерактивные справочники по теплоэнергетике и теплотехнике, каталоги энергетического оборудования, нормативно-правовая документация (ГОСТ, СНиП, СН, СО, РД и т.п.), типовые энергетические характеристики и их расчеты, тренажеры и программно-технические средства для производственного персонала энергетических предприятий, таблицы теплофизических свойств энергоносителей и т.д.
Литература: [1],[5],[8],[11],[13],[18].
Лекция 2
Тема: Математическое и физическое моделирование в теплоэнергетике. Процесс разработки и использования математических моделей.
План:Основные понятия математического и физического моделирования. Аналоговое моделирование. Процесс разработки и использования математических моделей. Методы и средства ускорения моделирования. Использование системного анализа при моделировании.
В дальнейшем будем рассматривать физическое моделированиеи аналоговое -из предметного, математическое моделирование-из знакового.
Введем ряд определений.
Математическая модель –приближенное описание какого-либо класса явлений внешнего мира, выраженное с помощью математической символики.
Математическое моделирование - процесс изучения явления с помощью математической модели.
Процесс математического моделирования можно подразделить на четыре этапа:
первый - формулирование законов, связывающих основные объекты модели, результат - запись в математических терминах сформулированных качественных представлений о связях между объектами модели;
второй – исследование математических задач, к которым приводят математические модели, основной вопрос – решение прямой задачи – получение в результате анализа модели выходных данных (теоретических следствий) для сопоставления их с результатами наблюдений изучаемых явлений;
третий - выяснение того соответствует ли принятая модель (гипотетичная) критерию практики, т.е. выяснение вопроса о том, согласуется ли результат наблюдений с теоретическими следствиями модели в пределах точности наблюдений. Задачи, в которых определяются характеристики модели таким образом, чтобы выходная информация была сопоставима в пределах точности наблюдений с результатами наблюдений – обратная задача;
четвертый – последующий анализ модели в связи с накоплением данных об изучаемых явлениях и модернизация модели.
Метод математического моделирования занимает ведущее место среди других методов исследования.
Физическое моделирование –экспериментальный метод научного исследования, состоящий в замене изучаемого физического процесса, явления или объекта другим, ему подобным – моделью. Геометрически подобная оригиналу модель имеет увеличенный или уменьшенный по сравнению с оригиналом размер. Модель может отличаться от реального процесса или явления количественными физическими характеристиками.
В основе физического моделирования лежит теория подобия и анализ размерностей.
Кроме прямого физического моделирования при исследовании различных физических процессов используются различные аналогии, позволяющие на основе однотипности математических уравнений, описывающих различные физические процессы, заменять изучение исследуемого процесса изучением другого процесса.
Например, при моделировании процессов теплообмена используется электротепловая аналогия, в которой исследуемое поле температур заменяется полем электрического потенциала в контуре CR (С- электрическая емкость, R-омическое сопротивление) .
При физическом моделировании сохраняется физическая природа исследуемого объекта. В случае моделирования аналогиями модель воспроизводит иное физическое явление, отличное по своей природе от натурного, но описываемого теми же уравнениями. Метод аналогий основан на формальной идентичности дифференциальных уравнений, описывающих различные по своей физической природе процессы (проявление единства природы).
На существование электрогидродинамической аналогии (ЭГДА) указывал еще Г.Кирхгоф в 1845 г. Метод ЭГДА основан на аналогии уравнений движения электрическоготока и уравнений потенциального течения жидкости. Метод магнитогазодинамической аналогии (МАГА) использует аналогию между уравнениями магнитного поля и уравнениями потенциального течения газа. Газогидравлическая аналогия (ГГА) основана на аналогии между уравнениями движения невязкой несжимаемой жидкости в открытом канале и уравнениями плоского потенциального движения газа. Ни один из указанных методов аналогий не позволяет моделировать силы вязкости. Электротепловая аналогия основана на замене поля температурполем электрического потенциала в CRконтуре, аналогом коэффициента температуропроводности является величина 1/CR. Гидротепловая аналогия дает возможность моделирования процессов стационарной теплопроводности на аналогии с безвихревым потоком идеальной жидкости.
Начало практическому применению метода ЭГДА к решению задач, связанных с движением жидкости было положено Д.Тома, который применил метод ЭГДА при изучении движения воды в направляющем аппарате колеса гидротурбины. В качестве электропроводного материала он использовал листы константана, в которых вырезались исследуемые решетки профилей направляющих аппаратов гидротурбин. Листы зажимались в медных шинах, к которым подводился электрический ток (постоянный). Широкое применение метод ЭГДА получил для решения задач обтекания турбинных и компрессорных решеток. На установке ЭГДА может быть непосредственно исследовано обтекания тел поступательно-циркуляционным потоком. Для решения практически важных задач необходимо уметь определять значение скоростей и давлений не только в контуре профиля, но и в любой точке исследуемой области поступательно-циркуляционного потока. Аналитическое решение такой задачи для одиночного профилятребует чрезвычайно сложных и громоздких вычислений. Для решетки профилей аналитическое решение подобной задачи неизвестно. Поэтому можно воспользоваться методом ЭГДА. Этим методом решались задачи обтекания тел плоским потоком сжимаемого газа с дозвуковой скоростью (используется электролитическая ванна с переменной глубиной электролита), нелинейные задачи газодинамики, обтекания крылового профиля, движения трехмерных потоков несжимаемой 
жидкости в проточной части турбомашин. Широкое применение нашел метод электрогидродинамической аналогии в вихревых полях (ВЭГА).
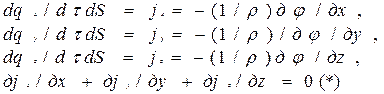 |
Для установления аналогов рассмотрим уравнения движения электрических зарядов в проводниках:
 | 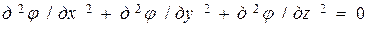 | ||
Подставив первые три уравнения в уравнение (*), получим:

В уравнениях j – плотность электрического тока, φ – электрический потенциал, ρ – удельное сопротивление проводника. Первые три уравнения представляют собой математическую запись закона Ома, уравнение, помеченное (*) – запись закона сохранения заряда.
Для потенциального течения несжимаемой жидкости:
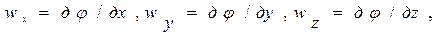
Уравнение неразрывности для несжимаемой жидкости имеет вид
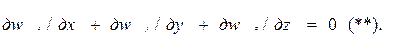
Подставив первые три уравнения в уравнение (**), получим
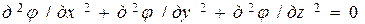 ,
,
где φ(x,y,z,τ) – потенциал скоростей.
Потенциал скоростей аналогичен электрическому потенциалу, удельная плотность электрического тока - скорости. Если область течения электрического тока подобна области течения жидкости, а граничные условия аналогичны, то интегралы уравнений Лапласа для этих функций будут отличаться лишь произвольными постоянными. Эквипотенциальные поверхности в электрическом поле тождественны эквипотенциальным поверхностям в потоке жидкости. Силовые линии электрического поля тождественны линиям тока в потоке жидкости.
Это трехмерный случай. В двумерном случае, при геометрическом подобии областей, когда граничные условия для электрического потенциала тождественны граничным условиям для потенциала скоростей, эквипотенциальные линии в электрическом поле тождественны эквипотенциальным линиям в потоке жидкости, силовые линии электрического поля тождественны линиям тока в жидкости.
Установка ЭГДА состоит из двух основных частей: моделии электрической схемы. Модельпредставляет собой область движения электрического тока, предназначенную воспроизводить исследуемую область движения жидкости. Для ее создания используют различные электропроводные материалы в сочетании с диэлектриками, образующими границы области. Электрическая схема ЭГДА состоит из питательной и измерительной цепей и контрольно-измерительных приборов. Все существующие установки ЭГДА работают по принципу мостовой или компенсационной схемы (или комбинированной).
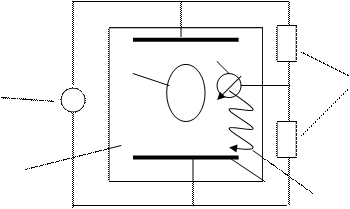

1 7
2 =
4 5
1-модель из диэлектрика, 2 - источник постоянного или переменного тока; 3 – водный раствор соли, 4 – шина; 5 – щуп, 6- резисторы, 7 – гальванометр
Рисунок 2.1 - Установка ЭГДА
Для идеальной жидкости функция тока удовлетворяет уравнению Лапласа. Гармонически сопряженная с ней функция – потенциал скоростей потока. Линии равных потенциалов и равных функций тока ортогональны. Распределение температуры в двумерном поле также подчиняется уравнению Лапласа, т.е. линии теплового потока и температурного потенциала аналогичны линиям тока и потенциалу скоростей идеального потока жидкости (гидротепловая аналогия).
Электротепловая аналогия заключается в том, что перенос тепла аналогичен переносу электрических зарядов (электропроводность аналогична теплопроводности).
Поток электрического заряда (сила тока):
I=Δq/Δτ = Δφ γ S/Δl= Δφ/RЭ
Тепловой поток:
qТ=ΔQ/Δτ = ΔТ λ S/Δl= ΔТ/RТ
Таким образом, тепловое сопротивление аналогично электрическому.
|

|

 Т1 RT= Δl/λS φ1 φ2
Т1 RT= Δl/λS φ1 φ2
 |  |
 Δl
Δl
Т2
RЭ= Δl/γS
Δl
Рисунок 2.2 - Одномерная модель стационарной теплопроводности через однослойную стенку и ее электрический аналог
|


 Т1
Т1
|
|


|
|
|





 Т2 Δl1 Δl2 Δl3
Т2 Δl1 Δl2 Δl3
 Т3 RЭ1 RЭ2 RЭ3
Т3 RЭ1 RЭ2 RЭ3
Т4
Δl1 Δl2 Δl3
RT1 RT2 RT3
Рисунок 2.3 - Одномерная модель стационарной теплопроводности через многослойную стенку и ее электрический аналог (последовательное соединение слоев)
При последовательном соединении слоев по аналогии с теорией электричества
qт=ΔT14/(Rт1+ Rт2+ Rт3).
Электротепловую аналогию можно использовать и для решения более сложных задач. Например, если теплопроводность протекает в материалах, расположенных параллельно.
|
|
 Т1 RЭ1
Т1 RЭ1




 RT1
RT1


|
|
 φ1 φ2
φ1 φ2

 RT2
RT2
 Т2 RЭ2
Т2 RЭ2
Рисунок 2.4 - Одномерная модель стационарной теплопроводности через многослойную стенку и ее электрический аналог (параллельное соединение слоев)
При этом по аналогии с теорией электричества
qт=ΔT12/(1/Rт1+ 1/Rт2).
К достоинству метода можно отнести: простоту электрической схемы, простоту измерения напряжения, большую точность результатов.
При разработке электрических моделей, имитирующих процессы теплопроводности, применяются два способа. В первом электрическая модель повторяет геометрию оригинальной тепловой системы и изготавливается из материала с непрерывной проводимостью. Такие модели – с непрерывными параметрами процесса. Во втором – тепловые системы заменяются электрическими цепями. Модели при этом будут с сосредоточенными параметрами процесса.
Метод исследования, основанный на идее физической аналогии, является наиболее сильным средством обобщенного анализа. Из курса физики вам известно, что существует тройная аналогия в явлениях переноса. Аналогия объединяет в единое целое разнородные явления, воспринимаемые как теплообмен, массообмен и гидродинамическое сопротивление. Аналогия является следствием единого молекулярного физического механизма процессов.
Уравнение Фурье (теплопроводность)
q = - λgrad T,
уравнение Фика (диффузия)
j = - D grad с,
уравнение Ньютона (вязкость)
σ = - η grad u.
Большинство промышленных технических объектов являются сложными системами. Характерные признаки сложной системы: невозможность рассмотрения отдельно каждого ее элемента (без установления связей с другими элементами и внешней средой); неопределенность в большом числе состояний системы; неопределенность достоверности информации; разнообразие вариантов достижения конечной цели функционирования системы; адаптивность (приспособляемость системы к возмущающим факторам воздействия среды).
Характерные особенности сложных систем вызывают необходимость использования в ходе создания их моделей методологии системного подхода.
Система -совокупность элементов, находящихся в отношениях и связях друг с другом, которая образует определенную целостность, единство.
Системные принципы:
- целостности (принципиальная не сводимость свойств системы к сумме свойств составляющих ее элементов и не выводимость из последних свойств целого);
- структурности (возможность описания системы через установление ее структуры, т.е. сети связей и отношений системы; обусловленность поведения системы не столько поведением ее отдельных элементов, сколько свойствами ее структуры);
- взаимозависимости системы и среды (система формирует и проявляет свои свойства в процессе взаимодействия со средой, являясь при этом активным, ведущим компонентом взаимодействия);
- иерархичности (каждый компонент системы в свою очередь может рассматриваться как система, а используемая в данном случае система представляет один из компонентов более широкой системы);
- множественности описания каждой системы.
Важной особенностью систем является передача в них информации и наличие процессов управления.
Системы бывают: замкнутые, открытые, статичные, динамичные, детерминированныеивероятностные.
Математическое описание модели в общем случае можно представить так
Y(τ)= F(X(τ), V(τ), S(τ), τ),

где F – закон функционирования системы;
X(τ) - входные параметры;
V(τ) - воздействия внешней среды;
S(τ) - собственные параметры системы;
Y(τ) - выходные параметры;
τ - время.
Параметры X,V,S часто называют экзогенными (независимыми), а Y - эндогенными (зависимыми).
Существует определенная последовательность реализации моделирования, показанная на схеме рис.2.5.
Основным количественным критерием адекватности модели является степень соответствия вычислительного эксперимента данным экспериментальных работ. При отсутствии последних или для предварительного анализа критерием можно считать непротиворечивость полученных результатов принятым при моделировании гипотезам и допущениям, а так же здравому смыслу.
Любая созданная модель должна удовлетворять ряду требований:
- адекватность ее объекту;
- доступность, простота и понятность для пользователя;
- универсальность (ее модули должны легко адаптироваться к другим модулям;
- точность (высокое совпадение результатов вычислительного эксперимента и параметров реального объекта);
- устойчивость и достоверность функционирования в широком диапазоне изменения рабочих параметров;
- открытость и модульность, способность к развитию без существенного изменения базового варианта;
- экономичность, реализуемая с помощью сравнительно простых алгоритмов и программ, не требующих больших ресурсов ВТ.
Многие из перечисленных требований противоречат друг другу, что требует от разработчиков добиться их оптимального сочетания в зависимости от поставленной цели моделирования.

Рисунок 2.5 – Схема последовательности реализации моделирования
Использование системного подхода в некоторой степени ускоряет процесс моделирования, поскольку предлагает разработчику методологию моделирования. Конкретизация этапов моделирования позволяет систематизировать виды его обеспечения: математическое, программное, информационное и техническое.
Можно предложить ряд средств ускорения моделирования в области этих видов обеспечения.
При решении задач моделирования сложных систем приходится периодически использовать разнообразную информацию, для тепловых процессов необходимы три группы данных: об индивидуальных свойствах газообразных и конденсированных веществ; о свойствах газообразных, жидких и твердых топлив; о химических реакциях и механизме их протекания. Выполнение требования адекватности математической модели невозможно без соблюдения требования максимальной достоверности этой информации. Для ее хранения используются банки данных (БнД). Преимущество использования БнД для информационного обеспечения при моделировании заключается в том, что с помощью системы управления базой данных (СУБД) программы прикладной области получают необходимую информацию из базы данных. Это позволяет представлять данные независимо от структуры прикладных программ в наиболее удобной логической форме и соответственно обеспечивает независимость прикладных программ от данных.
Принципиально новые возможности появляются при использовании в математическом моделировании и вычислительном эксперименте инструментальных систем (ИС). ИС принято называть программную систему, средства которой могут быть использованы для создания и развития пакетов прикладных программ (ППП) и прикладных программных комплексов (ППК) и для накопления базы знаний (БЗ), т.е. формализованной совокупности сведений о некоторой предметной области, содержащей данные о свойствах объектов, закономерностях процессов и явлений и правила использования этих знаний для принятия решения.
Оперативность моделирования обеспечивается следующими качествами ИС: возможностью оперирования языковыми конструкциями конкретной предметной области; автоматическим синтезом программ; возможностью оперативного рассмотрения различных вариантов математических моделей и их модификаций; организацией « дружественного интерфейса», состоящего в интерактивном диалоговом взаимодействии пользователя и системы с выполнением требований простоты и удобства общения для пользователя. Степень целесообразности использования ИС для решения задач математического моделирования зависит от их структуры, оценки уровня сложности модели, требований к ней, квалификации пользователя моделью.
Литература: [5],[13-18].
Лекция 3
Тема: Численные методы в математическом моделировании теплотехнических задач и их программная реализация. Методы интерполирования.
План: Элементы численных методов и их компьютерная реализация. Приближение функций.Интерполирование, полиномиальное интерполирование, интерполирование сплайнами, аппроксимация кривыми при решении задач приближения функций и расчета теплотехнических таблиц.
В настоящее время численные методы являются мощным математическим средством решения научно-технических задач и проблем. Это связано с тем, что в большинстве случаев невозможно получить точное аналитическое решение, а также со стремительным развитием компьютерной техники. Существует множество стандартных программ и объектно- ориентированных пакетов прикладных программ (ППП). Однако научным и инженерным работникам необходимо понимать сущность основных численных методов и алгоритмов, поскольку интерпретация результатов вычислительного эксперимента нетривиальна и требует специальных знаний особенностей применяемых методов.
Численный анализ является завершающей составляющей математической подготовки теплоэнергетика. Знание основ теории и способов реализации численных методов необходимо при проектной проработке и расчетном обосновании процессов, установок, агрегатов, систем теплоэнергетики и теплотехнологии.
Вы познакомитесь с методами аппроксимации функций, численного решения алгебраических и трансцендентных уравнений, а также систем линейных и нелинейных уравнений, задачами численного интегрирования и дифференцирования, методами решения обыкновенных дифференциальных уравнений, кратким введением в методы решения дифференциальных уравнений в частных производных и задач оптимизации. Практически все методы иллюстрируются алгоритмами и примерами их применения при решении теплотехнических задач. Рассматриваются вопросы реализации изучаемых численных методов на персональном компьютере (РС) с применением программных математических пакетов, которые широко используются в практических вычислениях. Закрепление теоретических знаний достигается при выполнении лабораторного практикума по дисциплине.
Дата добавления: 2017-09-19; просмотров: 3236;
