Основные методы решения тригонометрических уравнений.
1º. Уравнение вида 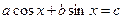 (a¹0, b¹0, c¹0) равносильно уравнению
(a¹0, b¹0, c¹0) равносильно уравнению 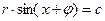 , где
, где 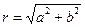 ,
, 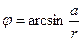 .
.
Пример 40. Решить уравнение.
Решение:
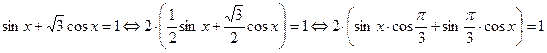
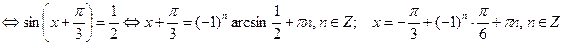 .
.
Ответ: 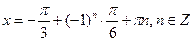 .
.
2º. Одним из основных методов решения тригонометрических уравнений, так же как и других видов уравнений, является метод подстановки (замены переменной).
Пример 41. Решить уравнение 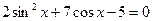 .
.
Решение: Так как 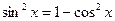 , то уравнение можно переписать следующим образом:
, то уравнение можно переписать следующим образом: 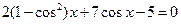 , т.е.
, т.е. 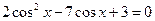 . Полагая
. Полагая 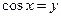 , приходим к квадратному уравнению
, приходим к квадратному уравнению 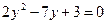 , откуда
, откуда 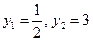 , и получаем совокупность двух простейших уравнений
, и получаем совокупность двух простейших уравнений 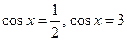 . Первое из них имеет решение
. Первое из них имеет решение 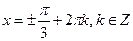 , а второе решений не имеет.
, а второе решений не имеет.
Ответ: 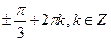 .
.
Метод замены переменной полезен при решении так называемых однородных уравнений, т.е. уравнений вида
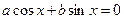 (однородное уравнение I порядка),
(однородное уравнение I порядка),
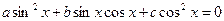 (однородное уравнение II порядка).
(однородное уравнение II порядка).
Если a¹0, то при делении обеих частей первого уравнения на 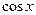 , а второго уравнения на
, а второго уравнения на 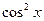 получаем алгебраические уравнения, решаемые подстановкой
получаем алгебраические уравнения, решаемые подстановкой 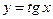 . Если a=0, то во втором уравнении
. Если a=0, то во втором уравнении 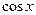 выносится за скобки.
выносится за скобки.
Пример 42. Решить уравнение 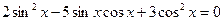 .
.
Решение: Разделив уравнение на 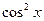 , получим
, получим 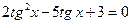 . Пусть
. Пусть 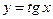 , тогда
, тогда 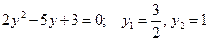 или:
или:
1) 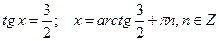 ;
;
2) 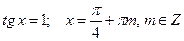 .
.
Ответ: 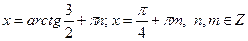 .
.
Замечание 1. Уравнение вида 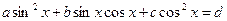 (d¹0) можно привести к однородному уравнению II порядка, положив
(d¹0) можно привести к однородному уравнению II порядка, положив 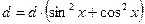 .
.
Замечание 2. Уравнение вида 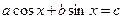 (c¹0) можно привести к однородному уравнению II порядка относительно
(c¹0) можно привести к однородному уравнению II порядка относительно 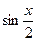 и
и 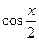 .
.
3º. При решении тригонометрических уравнений также часто используют метод разложения на множители.
Пример 43. Решить уравнение 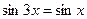 .
.
Решение: Все члены уравнения переносятся в левую часть, после чего левую часть уравнения раскладывают на множители:
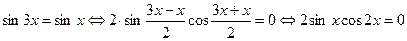 .
.
Значит, либо 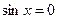 , откуда
, откуда 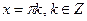 , либо
, либо 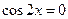 , откуда
, откуда 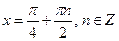 .
.
Ответ: 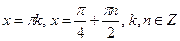 .
.
Заметим, что для разложения на множители могут применяться различные формулы: формулы разложения тригонометрических функций в произведение, формулы понижения степени, формулы преобразования произведения в сумму и др.
Пример 44. Решить уравнение 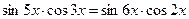 .
.
Решение: Согласно формуле (10.19) заменим произведение тригонометрических функций суммой, а затем воспользуемся формулой (10.15):
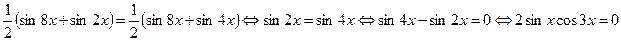
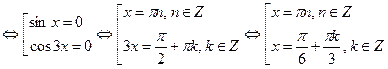 .
.
Ответ: 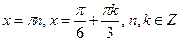 .
.
Пример 45. Решить уравнение 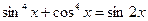 .
.
Решение: Это уравнение можно привести к квадратному относительно 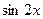 , понизив степень
, понизив степень 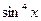 и
и 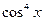 , но существует более короткий способ.
, но существует более короткий способ.
Дополним левую часть уравнения до полного квадрата суммы, для чего прибавим 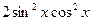 к обеим частям уравнения. Получим уравнение равносильное данному:
к обеим частям уравнения. Получим уравнение равносильное данному:
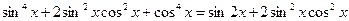 ;
;
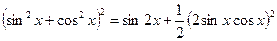 .
.
Применяя формулы (10.1) и (10.10), получаем: 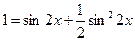 .
.
Пусть 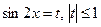 . Тогда
. Тогда 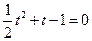 ;
; 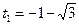 (не удовлетворяет условию
(не удовлетворяет условию 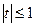 ),
), 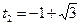 . Так как
. Так как 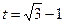 , то
, то 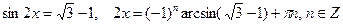 ,
,
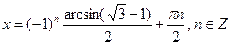 .
.
Ответ: 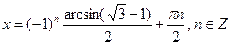 .
.
Таблица значений тригонометрических функций.
| Аргумент Функция | 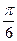
| 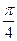
| 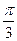
| 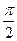
| π | 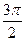
| 2π | |
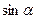
| 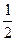
| 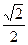
| 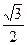
| -1 | ||||
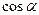
| 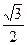
| 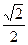
| 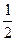
| -1 | ||||
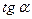
| 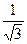
| 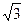
| — | — | ||||
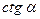
| — | 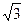
| 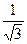
| — | — |
Дата добавления: 2017-09-19; просмотров: 276;
