Стереометрия. Многогранники.
1º. Призмой называется многогранник, поверхность которого состоит из двух равных многоугольников (оснований), расположенных в параллельных плоскостях, и параллелограммов (боковых граней), число которых равно числу сторон оснований.
Если l – длина бокового ребра, P – периметр основания, Sосн – площадь основания, Sсеч – площадь перпендикулярного сечения; Sбок – площадь боковой поверхности, V – объем, H – высота, то:
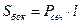 ;
; 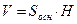 .
.
2º. Прямой называется призма, если ее боковые ребра перпендикулярны плоскостям оснований. Прямая призма называется правильной, если в ее основаниях лежат правильные многоугольники.
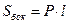
3º. Прямоугольным параллелепипедом называется прямая призма, основания которой – прямоугольники.
Если a, b, c – измерения параллелепипеда, d – диагональ, то:
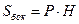 ;
; 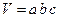 ;
; 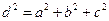 .
.
4º. Куб – прямоугольный параллелепипед, у которого все ребра равны (a – ребро).
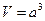 ;
; 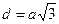
5º. Пирамидой называется многогранник, одна из граней которого – произвольный многоугольник (основание), а остальные грани (боковые грани) – треугольники, имеющие общую вершину.
Если Sосн – площадь основания, V – объем, H – высота, то:
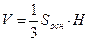 ;
;
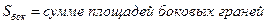 .
.
Если все боковые ребра пирамиды равны между собой, то:
1) боковые ребра образуют с плоскостью основания равные углы;
2) вершина пирамиды проектируется в центр описанной около основания окружности.
Если все боковые грани пирамиды наклонены к основанию под одним и тем же углом α, то:
1) апофемы всех боковых граней равны;
2) вершина пирамиды проектируется в центр окружности, вписанной в основание;
3) 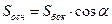 ;
; 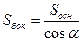 ;
;
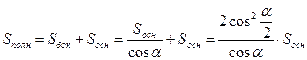
6º. Пирамида называется правильной, если ее основанием является правильный многоугольник, а высота проходит через его центр.
Если P – периметр основания, l – апофема, Sбок – площадь боковой поверхности, то:
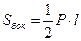 ;
; 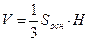 ;
; 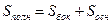 .
.
6º. Усеченной пирамидой называется часть пирамиды, заключенная между основанием и секущей плоскостью, параллельной основанию.
Для произвольной усеченной пирамиды: 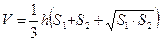 ,
,
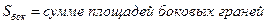 ,
,
для правильной усеченной пирамиды: 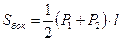 ,
,
где S1 и S2 – площади оснований, h - высота, V – объем, P1 и P2 – периметры оснований, l – апофема; Sбок – площадь боковой поверхности.
Пример 49. В основании пирамиды лежит треугольник со сторонами 6 см, 8 см, 10 см и все боковые ребра образуют с основанием углы по 45º. Тогда объем пирамиды равен:
1) 62 см3 2) 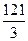 см3 3) 40 см3 4) 24 см3 5) 96 см3.
см3 3) 40 см3 4) 24 см3 5) 96 см3.
Решение.
Дано: MABC – пирамида, 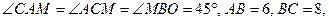
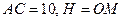 . Найти
. Найти 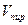 .
.
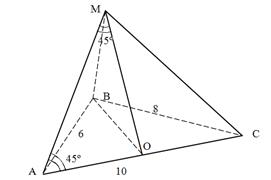
Так как 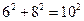 , т.е.
, т.е. 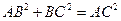 , то по теореме обратной теореме Пифагора – ΔABC – прямоугольный,
, то по теореме обратной теореме Пифагора – ΔABC – прямоугольный, 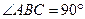 , AB, BC – его катеты, AC – гипотенуза. По условию все боковые ребра пирамиды наклонены под одним и тем же углом к плоскости основания, значит, вершина пирамиды проектируется в центр описанной около основания окружности, т.е. в середину гипотенузы ΔABC.
, AB, BC – его катеты, AC – гипотенуза. По условию все боковые ребра пирамиды наклонены под одним и тем же углом к плоскости основания, значит, вершина пирамиды проектируется в центр описанной около основания окружности, т.е. в середину гипотенузы ΔABC.
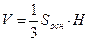 ,
, 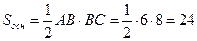 .
.
В ΔAOM ( 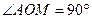 ) острые углы
) острые углы 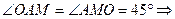 треугольник равнобедренный,
треугольник равнобедренный, 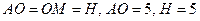 . Таким образом,
. Таким образом,
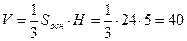 .
.
Ответ: 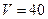 см3 (№3 – правильный ответ).
см3 (№3 – правильный ответ).
Пример 50. Пусть в треугольной пирамиде все боковые грани образуют с плоскостью основания углы по 60º, и в основание вписан круг площадью 9π см2. Тогда высота пирамиды равна:
1) 3 см 2) 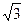 см 3)
см 3) 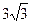 см 4) 9 см 5)
см 4) 9 см 5) 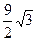 см.
см.
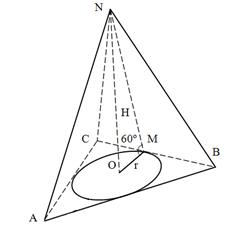
Решение. Пусть радиус круга, вписанного в основание пирамиды, - r. Тогда площадь круга S равна: 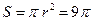 . Отсюда
. Отсюда 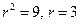 . Из прямоугольного треугольника OMN находим:
. Из прямоугольного треугольника OMN находим: 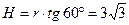 .
.
Ответ: высота пирамиды равна 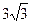 см (№3 – правильный ответ).
см (№3 – правильный ответ).
Пример 51. В основании прямоугольного параллелепипеда лежит квадрат площадью 16 см2. Через одну из сторон нижнего основания и противоположную сторону верхнего проведена плоскость. Площадь полученного сечения равна 20 см2. При этом полная поверхность параллелепипеда равна:
1) 96 см2 2) 48 см2 3) 40 см2 4) 80см2 5) 56 см2.
 Решение.
Решение.
Дано: ABCDA1B1C1D1 – прямоугольный параллелепипед, ABCD – квадрат, 
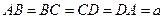 .
. 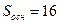 см2, ABC1D1 – сечение параллелепипеда,
см2, ABC1D1 – сечение параллелепипеда, 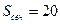 см2. Найти
см2. Найти 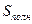 .
.
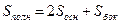 .
.
По условию 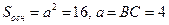 .
.
Тогда 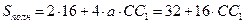 .
.
Вычислим СС1. По условию 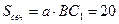 ,
, 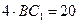 ,
, 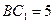 .
.
Из ΔBCC1: 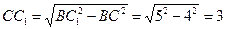 .
.
Окончательно, 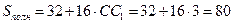 .
.
Ответ: 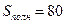 см2 (№4 – правильный ответ).
см2 (№4 – правильный ответ).
Дата добавления: 2017-09-19; просмотров: 220;
