Дидактический материал.

1. Найти диаметр шара, если его объем равен .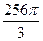

1) 8 2) 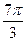3) 9 4) 3π 5) 7

2. Площадь боковой поверхности прямого кругового цилиндра равна 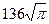, а его объем равен 17. Найти высоту цилиндра.

1) 272 2) 68π 3) 262 4) 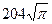5) 208

3. В конус вписан шар радиуса 2 см. Угол между образующей конуса и его высотой равен 30º. Боковая поверхность конуса равна:

1) 24π см² 2) 4π см² 3) 16π см² 4) 18π см² 5) 20π см²

4. Пусть шар вписан в усеченный конус, радиус меньшего основания которого равен 10 см, а радиус большего основания – 14 см. Тогда площадь поверхности шара равна:

1) 48π см² 2) 280π см² 3) 144π см² 4) 560π см² 5) 16π см²

5. Расстояние между тремя точками сферы равны 26, 24 и 10 см, а площадь сферы 900π см², тогда расстояние от проходящей через них плоскости до центра сферы равно:

1) 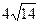2) 56 3) 56π 4) 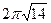5) .

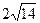6. Найти площадь боковой поверхности прямого кругового цилиндра, если его образующая равна 18, а площадь оснований 36π.

1) 126π 2) 90π 3) 72π 4) 108π 5) 216π

7. Если образующая конуса равна 6 см, а угол при вершине осевого сечения равен 60º, то площадь поверхности шара, вписанного в этот конус, равна:

1) 12π см² 2) 6 см² 3) 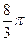см² 4) 18π см² 5) 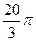см²

8. В сферу радиуса 10см вписан конус, образующая которого наклонена к плоскости основания под углом 45º. При этом площадь боковой поверхности конуса равна:

1) 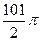см² 2) 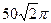см² 3) 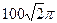см² 4) 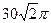см² 5) 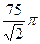см².

9. Шар, площадь поверхности которого равна 144π см², вписан в усеченный конус, образующая которого равна 20 см. При этих условиях площадь меньшего основания усеченного конуса равна:

1) 2π см² 2) 4π см² 3) 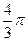см² 4) 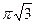см² 5) 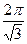см².

10. В сферу вписан прямоугольный параллелепипед с измерениями 6 см, 3 см и 2 см. Тогда радиус сферы равен:

1) 4 см 2) 3 см 3) 6 см 4) 2,5 см 5) 3,5 см.