Дидактический материал.
Укажите множество решений неравенства:
1. 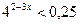 ; 2.
; 2. 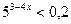 ; 3.
; 3. 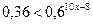 ;
;
4. 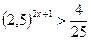 ; 5.
; 5.  .
.
6. При каких значениях x точки графика функции 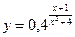 лежат ниже прямой
лежат ниже прямой 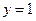 ?
?
7. При каких значениях x точки графика функции  лежат не ниже прямой
лежат не ниже прямой 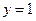 ?
?
Решите неравенство:
8. 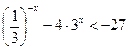 ; 9.
; 9.  ; 10.
; 10. 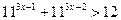 ;
;
11. 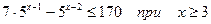 ; 12.
; 12. 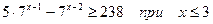 .
.
13. Укажите наибольшее целое решение неравенства 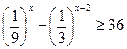 .
.
14. Найдите произведение наибольшего целого и наименьшего целого решений неравенства 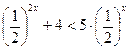 .
.
Решите неравенство:
15. 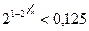 ; 16.
; 16. 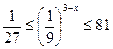 ; 17.
; 17. 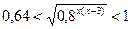 ;
;
18. 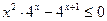 ; 19.
; 19. 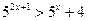 ; 20.
; 20.  ;
;
21. 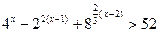 ; 22.
; 22. 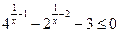 ; 23.
; 23. 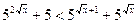 ;
;
24. 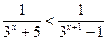 ; 25.
; 25.  ; 26.
; 26. 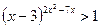 .
.
Найдите область определения функции:
27.  ; 28.
; 28. 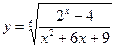 .
.
29. Найдите множество значений аргумента, при которых значения каждой из функций больше 3:
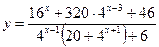 и
и 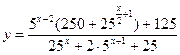 .
.
Ответы: 11. 3; 12. 3; 13. -3; 14. 1; 15. (0; 0,5); 16. [1,5; 5]; 17. (-1; 0)U(3; 4); 18. [-2; 2]; 19. (0; +∞); 20. (0; 1); 21. (3; +∞); 22. (-∞; 0)U(0,5; +∞); 23. (0; 1); 24. (-1; 1); 25. (0; 2]; 26. (3; 3,5)U (4; +∞); 27. (-∞; 3)U{5}; 28. [2; +∞); 29. (-∞; log5(5 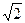 -5)).
-5)).
Тема №9.
Логарифмы.
1º. Логарифмом числа b по основанию a (где 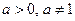 ) называется показатель степени, в которую надо возвести a, чтобы получить число b.
) называется показатель степени, в которую надо возвести a, чтобы получить число b.
Логарифм числа b по основанию a обозначается символом logab. В записи logab число a называют основанием логарифма, число b – логарифмируемым числом.
Равенство  означает, что
означает, что 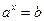 .
.
2º. Основным логарифмическим тождеством называется равенство  , которое справедливо при
, которое справедливо при 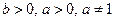 .
.
Например, 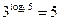 .
.
3º. Логарифм по основанию 10 называется десятичным логарифмом и обозначается lg вместо log10. Логарифм по основанию e (e=2,712828…) называется натуральным логарифмом и обозначается ln вместо loge.
4º. Основные свойства логарифмов:
1) 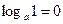 ;
;
2) 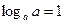 ;
;
3) 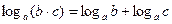 (логарифм произведения), где
(логарифм произведения), где 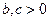 ;
;
4) 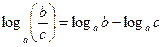 (логарифм частного), где
(логарифм частного), где 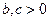 ;
;
5) 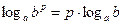 (логарифм степени), где
(логарифм степени), где 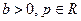 ;
;
Замечание. Если b<0, а p – четное целое число, то справедлива формула:

6)  (формула перехода к другому основанию логарифма).
(формула перехода к другому основанию логарифма).
В частности,  .
.
Пример 29. Найти 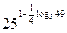 .
.
Решение: Воспользуемся основным логарифмическим тождеством и свойством «логарифм степени».
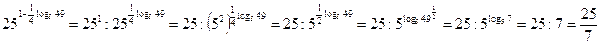 .
.
Пример 30. Вычислить  .
.
Решение: Для решения данного примера необходимо использовать все свойства логарифмов:
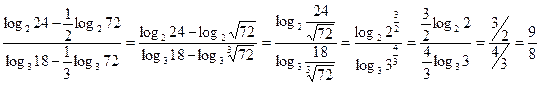 .
.
Пример 31. Вычислить 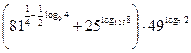 .
.
Решение: Для решения данного примера используются все свойства логарифмов, а также основное логарифмическое тождество:
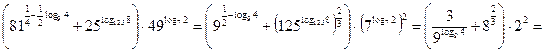
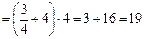 .
.
Ответ: 19.
Пример 32. Найти 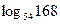 , если
, если  и
и 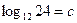 .
.
Решение: Разложим числа 168, 54, 24 и 12 на множители:
 . Полагая
. Полагая 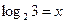 и
и 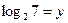 , выразим через x и y все логарифмы, содержащиеся в условии:
, выразим через x и y все логарифмы, содержащиеся в условии:
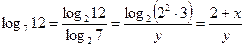 ;
;
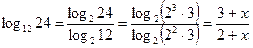 ;
;
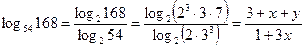 .
.
Согласно условию для определения x и y получаем систему уравнений:
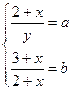 , решая которую находим
, решая которую находим  ,
, 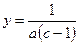 .
.
Подставим найденные значения x и y в равенство для определения 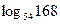 , получим ответ:
, получим ответ: 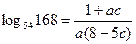 .
.
5º. Логарифмирование – это преобразование, при котором логарифм выражения с переменными приводится к сумме или разности логарифмов переменных.
Потенцирование – это преобразование, обратное логарифмированию.
Пример 33. Дано 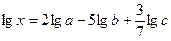 , где
, где 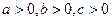 .
.
Найти выражение для x.
Решение: Потенцируя, получим:
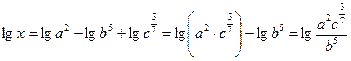 ,
, 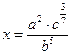 .
.
Дата добавления: 2017-09-19; просмотров: 265;
