Иррациональные уравнения.

1º. Иррациональным называют уравнение, в котором переменная содержится под знаком корня.

При решении иррациональных уравнений применяют 2 метода: метод возведения в степень обеих частей уравнения и метод введения новой переменной (замены переменной).

2º. Метод возведения обеих частей уравнения в одну и ту же степень состоит в следующем:

а) преобразуют заданное иррациональное уравнение к виду ;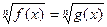

б) возводят обе части полученного уравнения в n-ую степень: ;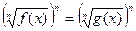

в) учитывая, что 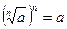, получают уравнение 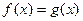и решают его.

3º. Следует учитывать, что при возведении обеих частей уравнения в четную степень возможно появление посторонних корней. В этом случае обязательна проверка найденных корней путем их подстановки в исходное уравнение.

Пример 16. Решить уравнение .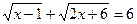

Решение: Преобразуем уравнение к виду 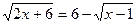и возведем обе части его в квадрат. Получим:

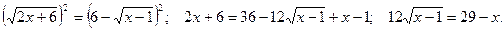
Еще раз возведем обе части уравнения в квадрат:

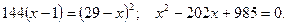
Откуда получим: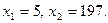

Проверка: 1) При x=5 имеем: 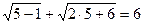. Таким образом, x=5 является корнем заданного уравнения.

2) 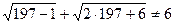. Таким образом, x=197 – посторонний корень.

Ответ: 5.

4º. Метод замены переменной продемонстрируем на примере.

Пример 17. Решить уравнение .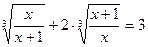

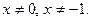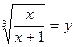Решение: Область определения уравнения: Пусть , тогда 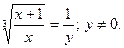Поэтому 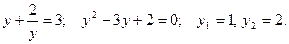Отсюда:

1) 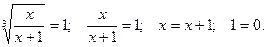Получили неверное числовое равенство, значит, в этом случае нет корней.

2)

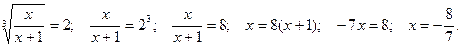
Ответ: -8/7.