Линейные однородные уравнения. Метод Эйлера.
Дифференциальное уравнение вида

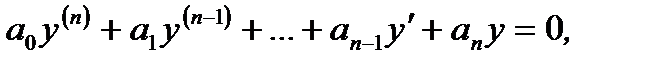 (7.153)
(7.153)
линейное относительно неизвестной функции 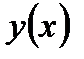 и ее производных до порядка
и ее производных до порядка 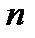 включительно, называется линейным однородным уравнением
включительно, называется линейным однородным уравнением 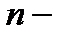 го порядка с постоянными действительными коэффициентами
го порядка с постоянными действительными коэффициентами 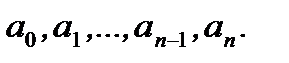
Известно, что если линейная комбинация функций 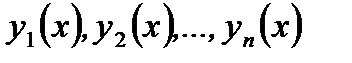 рана нулю, то есть
рана нулю, то есть
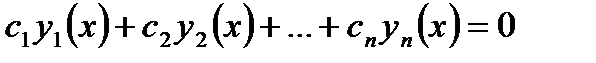 (7.154)
(7.154)
только если все 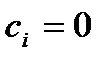
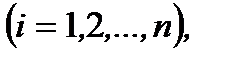 то функции
то функции 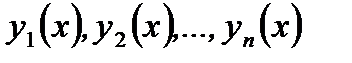 называются линейно независимыми. А если (7.154) удовлетворяется хотя бы при
называются линейно независимыми. А если (7.154) удовлетворяется хотя бы при 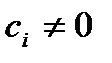
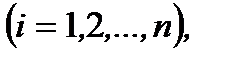 то функции
то функции
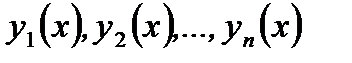 называются линейно зависимыми.
называются линейно зависимыми.
Пример 7.23.Функции 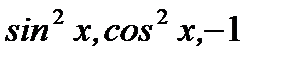 являются линейно зависимыми функциями, так как для любого действительного значения
являются линейно зависимыми функциями, так как для любого действительного значения 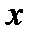 имеет место соотношение
имеет место соотношение
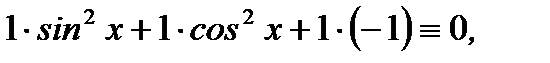 (7.155)
(7.155)
где даже все коэффициенты при 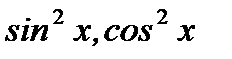 и
и 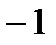 не равны нулю. Ниже приведем примеры линейно независимых функций без доказательства.
не равны нулю. Ниже приведем примеры линейно независимых функций без доказательства.
1. 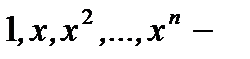 линейно независимы.
линейно независимы.
2. 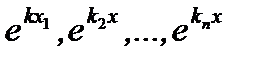 при
при 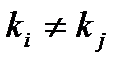
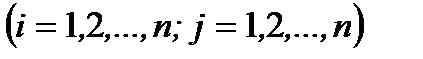 линейно независимы.
линейно независимы.
3. 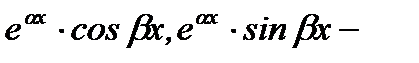 линейно независимы.
линейно независимы.
Если функции 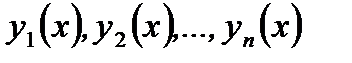 являются линейно независимыми частными решениями уравнения (7.153) (они составляют фундаментальную систему решений), то их линейная комбинация с произвольными постоянными коэффициентами является общим решением того же уравнения (7.153), то есть
являются линейно независимыми частными решениями уравнения (7.153) (они составляют фундаментальную систему решений), то их линейная комбинация с произвольными постоянными коэффициентами является общим решением того же уравнения (7.153), то есть
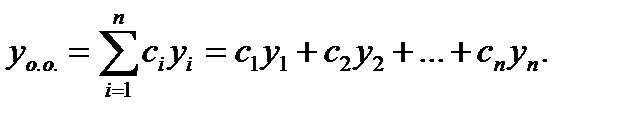 (7.156)
(7.156)
Далее ограничимся рассмотрением линейного дифференциального уравнения с постоянными действительными коэффициентами второго порядка, то есть уравнением вида
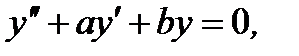 (7.157)
(7.157)
где 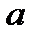 и
и 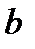 действительные числа. Следуя методу Эйлера частные решения (7.157) будем искать в виде:
действительные числа. Следуя методу Эйлера частные решения (7.157) будем искать в виде: 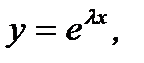 где
где 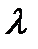 пока неизвестные действительные или комплексные числа. После подстановки
пока неизвестные действительные или комплексные числа. После подстановки 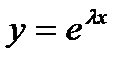 и ее производных
и ее производных 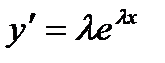 и
и 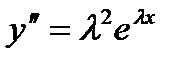 в уравнение (7.157), и после деления обеих частей уравнения на
в уравнение (7.157), и после деления обеих частей уравнения на 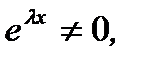 получим алгебраическое уравнение второй степени для определения характеристических чисел
получим алгебраическое уравнение второй степени для определения характеристических чисел 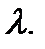 Оно имеет вид
Оно имеет вид
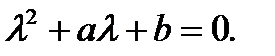 (7.158)
(7.158)
Полученное уравнение (7.158) называется характеристическим уравнением. Структура фундаментальной системы решений и соответствующего ей общего решения уравнения (7.157) зависит от значений корней характеристического уравнения (7.158). Возможны следующие случаи:
1. Корни 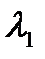 и
и 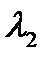 характеристического уравнения действительны и различны, то есть
характеристического уравнения действительны и различны, то есть
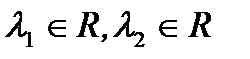 и
и 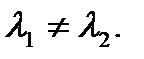 Тогда частные решения
Тогда частные решения 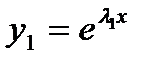 и
и 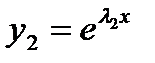 линейно независимы и общее решение уравнения (7.157) будет иметь вид
линейно независимы и общее решение уравнения (7.157) будет иметь вид
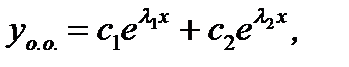 (7.159)
(7.159)
где 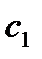 и
и 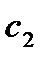 произвольные постоянные.
произвольные постоянные.
Пример 7.24.Решить уравнение
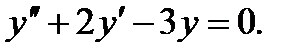 (7.160)
(7.160)
Решение.Решение (7.160) ищем в виде 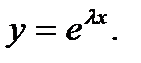 Подставляя
Подставляя 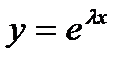 в (7.160), получим характеристическое уравнение
в (7.160), получим характеристическое уравнение
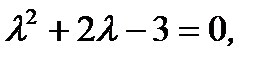 (7.161)
(7.161)
которое имеет два различных действительных корня 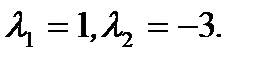 Тогда совокупность функций
Тогда совокупность функций 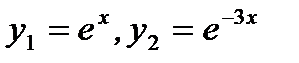 составляют фундаментальную систему решений, а функция
составляют фундаментальную систему решений, а функция 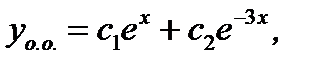 где
где 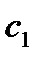 и
и 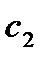 произвольные постоянные, является общим решением уравнения (7.160).
произвольные постоянные, является общим решением уравнения (7.160).
Ответ: 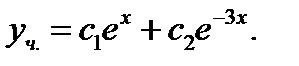
2. Корни 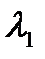 и
и 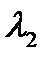 характеристического уравнения действительны и равны, то есть
характеристического уравнения действительны и равны, то есть 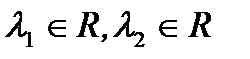 и
и 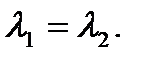 Очевидно, что
Очевидно, что 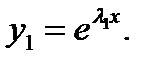 Можно показать, что второе независимое решение в этом случае выражается формулой
Можно показать, что второе независимое решение в этом случае выражается формулой 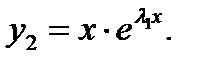 Тогда согласно (7.156)
Тогда согласно (7.156)
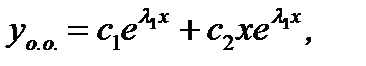 (7.162)
(7.162)
Пример 7.25.Решить уравнение
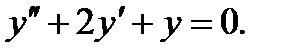 (7.163)
(7.163)
Решение. Ищем решение этого уравнения в виде 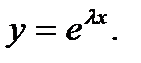 Характеристическое уравнение
Характеристическое уравнение 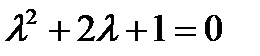 имеет два действительных и равных корня
имеет два действительных и равных корня 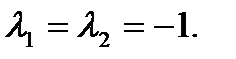 Тогда
Тогда 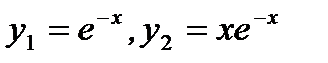 и
и 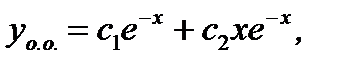 где
где 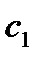 и
и 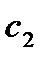 произвольные постоянные.
произвольные постоянные.
Ответ: 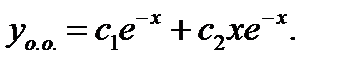
3. Корни 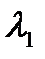 и
и 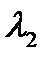 характеристического уравнения комплексны, то есть
характеристического уравнения комплексны, то есть 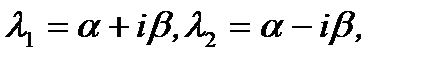 где
где 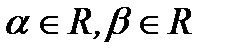 (так как имеем дифференциальное уравнение с действительными коэффициентами, то если один корень комплексный, то второй корен будет комплексно сопряженный). В этом случае два независимых решения уравнения получим, подставляя в
(так как имеем дифференциальное уравнение с действительными коэффициентами, то если один корень комплексный, то второй корен будет комплексно сопряженный). В этом случае два независимых решения уравнения получим, подставляя в 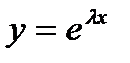
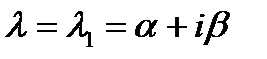 и преобразуя полученное выражение, пользуясь известной формулой Эйлера
и преобразуя полученное выражение, пользуясь известной формулой Эйлера 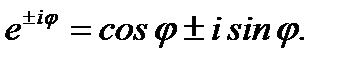 На самом деле имеем
На самом деле имеем
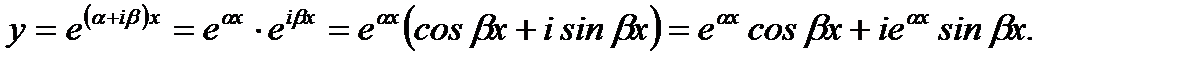 (7.164)
(7.164)
Как известно, в этом случае 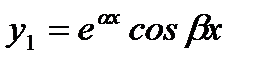 и
и 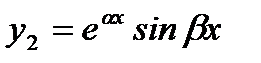 являются линейно независимыми функциями и представляют фундаментальную систему решений исходного уравнения. Тогда
являются линейно независимыми функциями и представляют фундаментальную систему решений исходного уравнения. Тогда 
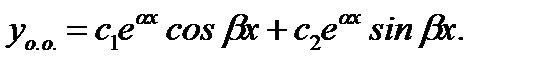 (7.165)
(7.165)
Пример 7.26.Решить уравнение
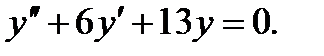 (7.166)
(7.166)
Решение. Характеристическое уравнение 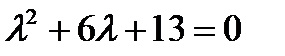 имеет комплексно сопряженные корни
имеет комплексно сопряженные корни
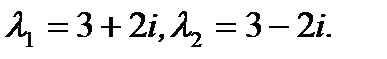 (7.167)
(7.167)
Тогда двум линейно независимым решениям
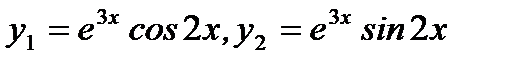 (7.168)
(7.168)
Соответствует общее решение уравнения (7.166) вида
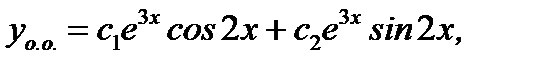 (7.169)
(7.169)
где 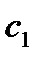 и
и 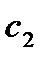 произвольные постоянные.
произвольные постоянные.
Ответ: 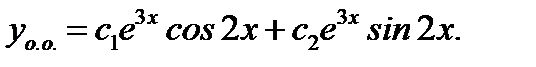
Дата добавления: 2018-11-25; просмотров: 550;
