Уравнение Бернулли.
Дифференциальное уравнение первого порядка вида
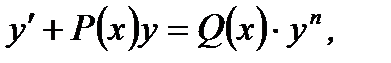 (7.76)
(7.76)
где 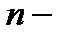 некоторое действительное число
некоторое действительное число 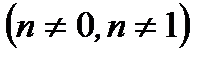 , а
, а 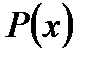 и
и 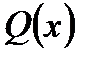 заданные непрерывные функции, называется уравнением Бернулли (при
заданные непрерывные функции, называется уравнением Бернулли (при 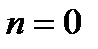 получаем уравнение с разделяющимися переменными, при
получаем уравнение с разделяющимися переменными, при 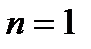 получаем линейное неоднородное уравнение). Уравнение Бернулли сводится к линейному неоднородному уравнению первого порядка заменой переменной
получаем линейное неоднородное уравнение). Уравнение Бернулли сводится к линейному неоднородному уравнению первого порядка заменой переменной
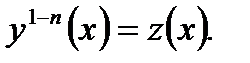 (7.77)
(7.77)
Отметим, что новую переменную удобно ввести после деления обеих частей уравнения
(7.76) на 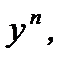 считая
считая 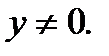 Но
Но 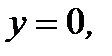 как видно из (7.76), является решением уравнения Бернулли. Это решение не потеряется, а получится из общего решения при определенном значении произвольной постоянной.
как видно из (7.76), является решением уравнения Бернулли. Это решение не потеряется, а получится из общего решения при определенном значении произвольной постоянной.
Пример 7.15.Решить уравнение Бернулли
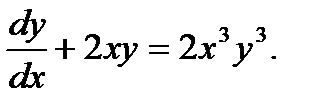 (7.78)
(7.78)
Решение.Разделив обе части уравнения (7.78) на 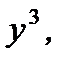 считая
считая 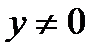 , и введя новую переменную
, и введя новую переменную
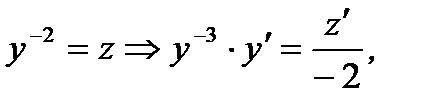 (7.79)
(7.79)
получим линейное неоднородное уравнение первого порядка относительно новой переменной 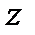 (отметим, что новая переменная есть функция от
(отметим, что новая переменная есть функция от 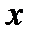 )
)
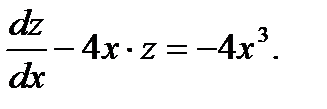 (7.80)
(7.80)
Соответствующее однородное уравнение
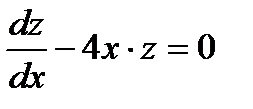 (7.81)
(7.81)
имеет решение
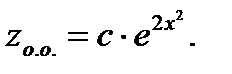 (7.82)
(7.82)
где 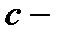 произвольная постоянная. Частное решение неоднородного уравнения (7.80) ищем в виде
произвольная постоянная. Частное решение неоднородного уравнения (7.80) ищем в виде
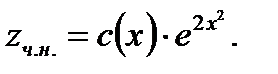 (7.83)
(7.83)
Подставляя (7.83) в (7.80) с учетом того, что
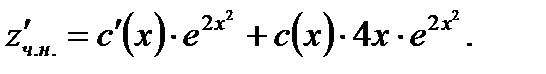 (7.84)
(7.84)
получим
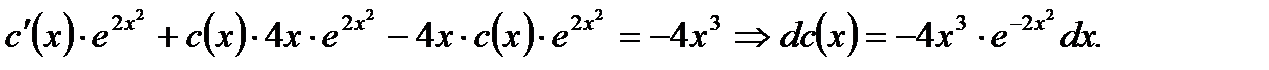 (7.85)
(7.85)
Интегрирование последнего приводит к следующему выражению для 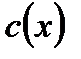
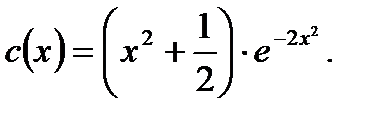 (7.86)
(7.86)
Тогда согласно (7.83), (7.52) и (7.79), общее решение исходного уравнения (7.78) имеет вид
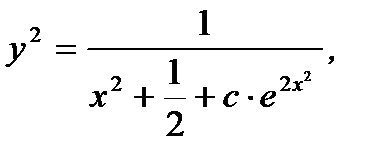 (7.87)
(7.87)
где 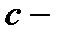 произвольная постоянная. Отметим, что решение
произвольная постоянная. Отметим, что решение 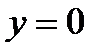 исходного уравнения получается из общего решения (7.87) при
исходного уравнения получается из общего решения (7.87) при 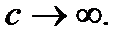
Ответ: 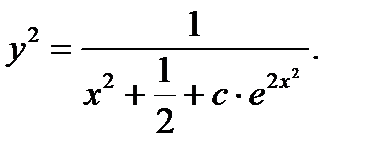
Пример 7.16.Пусть 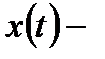 число особей в популяции в момент времени
число особей в популяции в момент времени 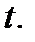 Тогда если
Тогда если 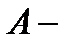 число особей в популяции, рождающихся в единицу времени,
число особей в популяции, рождающихся в единицу времени, 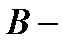 число особей, умирающих в единицу времени, то скорость изменения
число особей, умирающих в единицу времени, то скорость изменения 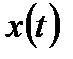 будет иметь вид
будет иметь вид
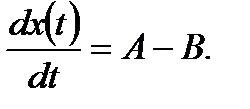
Если считать процесс изменения популяции нелинейным, что соответствует реальному процессу, то можно предположить, что, например, 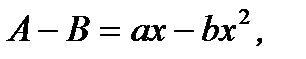 где
где 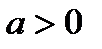 и
и 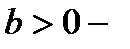 заданные постоянные. Тогда можно сказать, что процесс изменения популяции описывается следующим дифференциальным уравнением
заданные постоянные. Тогда можно сказать, что процесс изменения популяции описывается следующим дифференциальным уравнением
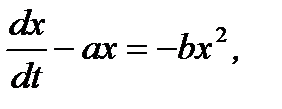 (7.88)
(7.88)
что является уравнением Бернулли. Найдем решение этого уравнения при заданным начальным условием Коши
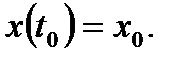 (7.89)
(7.89)
Решение.Для решенияуравнения Бернулли (7.88) делим обе части уравнения на 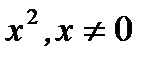 и вводим новую переменную формулой
и вводим новую переменную формулой 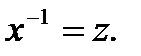 После этого уравнение (7.88) преобразуется к линейному неоднородному уравнению первого порядка относительно неизвестной функции
После этого уравнение (7.88) преобразуется к линейному неоднородному уравнению первого порядка относительно неизвестной функции 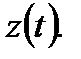 Решая полученное уравнение (см. пункт 7.1.4) с учетом условия Коши и в ответе переходя к переменной
Решая полученное уравнение (см. пункт 7.1.4) с учетом условия Коши и в ответе переходя к переменной 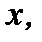 получим
получим
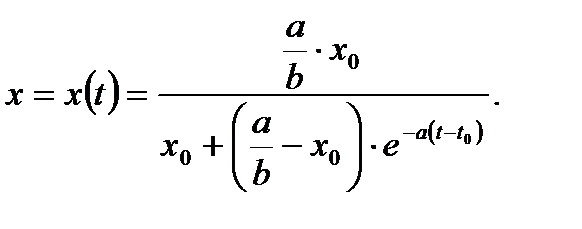 (7.90)
(7.90)
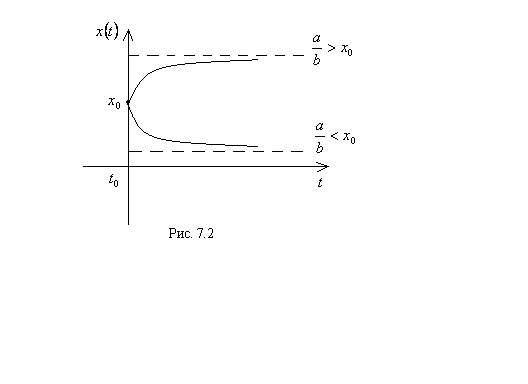
Как следует из решения (7.90) исходного уравнения 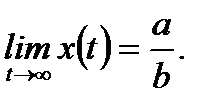 На рисунке 7.2 приведена интегральная кривая решения (7.90). Верхняя половина кривой соответствует случаю
На рисунке 7.2 приведена интегральная кривая решения (7.90). Верхняя половина кривой соответствует случаю 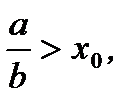 нижняя половина кривой соответствует случаю
нижняя половина кривой соответствует случаю 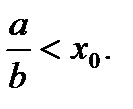
Ответ: 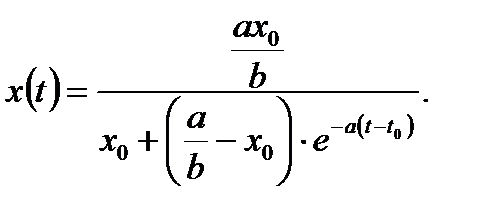
Дата добавления: 2018-11-25; просмотров: 618;
