Однородные уравнения.
Однородными дифференциальными уравнениями первого порядка называются уравнения вида
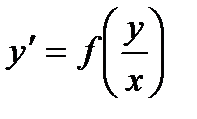 либо
либо 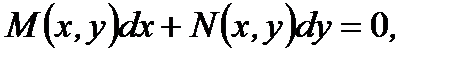 (7.29)
(7.29)
где 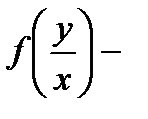 нулевой степени однородная функция относительно
нулевой степени однородная функция относительно 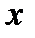 и
и 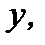 а
а 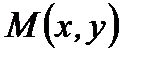 и
и 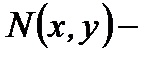 однородные функции относительно
однородные функции относительно 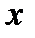 и
и 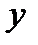 одинаковой степени. Напомним, что функция двух переменных
одинаковой степени. Напомним, что функция двух переменных 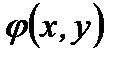 называется однородной функцией степени
называется однородной функцией степени 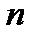 относительно
относительно 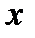 и
и 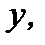 если для любого действительного числа
если для любого действительного числа 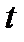 справедливо соотношение
справедливо соотношение
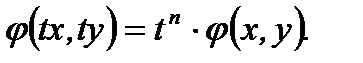 (7.30)
(7.30)
Например, функция 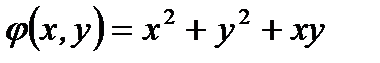 относительно
относительно 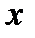 и
и 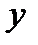 второй степени однородная функция, так как
второй степени однородная функция, так как

А функция 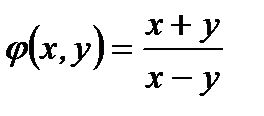 относительно
относительно 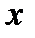 и
и 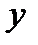 нулевой степени однородная функция, так как
нулевой степени однородная функция, так как
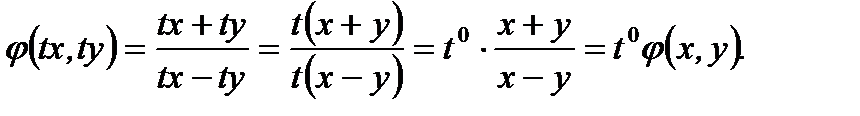
Однородные уравнения (7.29) приводятся к уравнениям с разделяющимися переменными заменой 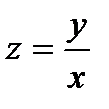 с учетом того, что
с учетом того, что 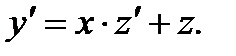
Пример 7.10.Решить уравнение
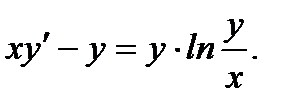 (7.31)
(7.31)
Решение.Разрешив (7.31) относительно производной 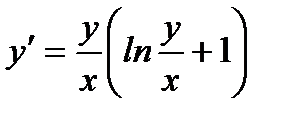 и убедившись, что данное уравнение является однородным, делаем замену переменной
и убедившись, что данное уравнение является однородным, делаем замену переменной 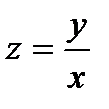 . Отсюда
. Отсюда
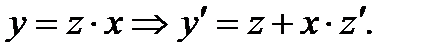 (7.32)
(7.32)
Подставляя значения 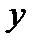 и
и 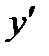 из (7.32) в исходное уравнение, его можно преобразовать к уравнению с разделяющимися переменными
из (7.32) в исходное уравнение, его можно преобразовать к уравнению с разделяющимися переменными
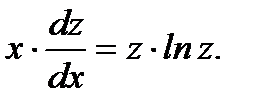 (7.33)
(7.33)
Разделив переменные, считая, что 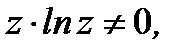 получим уравнение с разделенными переменными
получим уравнение с разделенными переменными
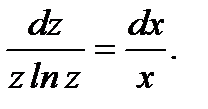 (7.34)
(7.34)
Интегрируя (7.34), получим
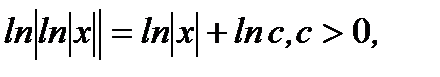
или
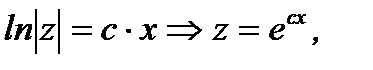 (7.35)
(7.35)
где 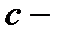 произвольная постоянная. Переходя в (7.35) к функции
произвольная постоянная. Переходя в (7.35) к функции 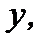 получим общее решение исходного дифференциального уравнения в виде
получим общее решение исходного дифференциального уравнения в виде
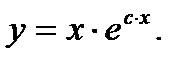 (7.36)
(7.36)
Заметим, что при делении обеих частей уравнения (7.34) на 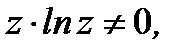 можно было потерять решение
можно было потерять решение 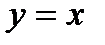 исходного уравнения (7.31). Из полученного общего решения (7.36) видно, что данное решение получается при значении постоянной
исходного уравнения (7.31). Из полученного общего решения (7.36) видно, что данное решение получается при значении постоянной 
Ответ: 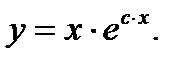
Пример 7.11.Решить уравнение
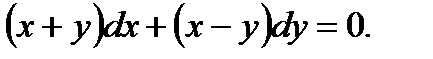 (7.37)
(7.37)
Решение.Здесь 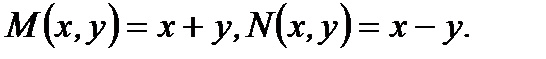 Так как
Так как 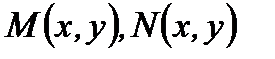 являются однородными функциями первой степени относительно
являются однородными функциями первой степени относительно 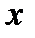 и
и 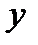 , то уравнение (7.37) является однородным уравнением первого порядка. После замены переменной
, то уравнение (7.37) является однородным уравнением первого порядка. После замены переменной 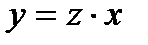 с учетом того, что
с учетом того, что 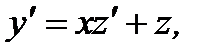 приходим к уравнению с разделяющимися переменными вида
приходим к уравнению с разделяющимися переменными вида
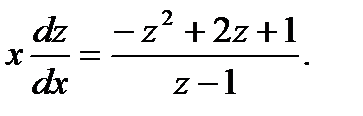 (7.38)
(7.38)
Разделив переменные в (7.38) и интегрируя, получим общий интеграл уравнения (7.37)
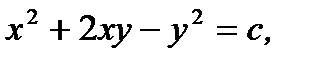 (7.39)
(7.39)
где 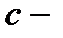 произвольная постоянная.
произвольная постоянная.
Ответ: 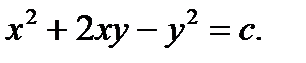
К однородному дифференциальному уравнению первого порядка приводятся уравнения вида
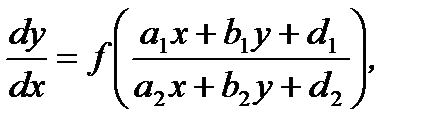 (7.40)
(7.40)
где  действительные постоянные.
действительные постоянные.
Если прямые 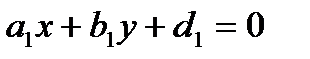 и
и 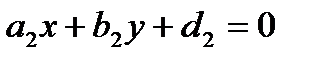 пересекаются в точке с координатами
пересекаются в точке с координатами 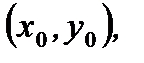 то введением новых переменных
то введением новых переменных 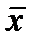 и
и 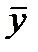 формулами
формулами
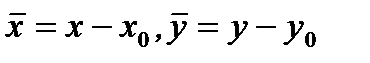 (7.41)
(7.41)
уравнение (7.40) приводится к однородному уравнению. Если же прямые параллельны, то подстановка 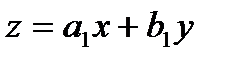 приводит к уравнению с разделяющимися переменными.
приводит к уравнению с разделяющимися переменными.
Пример 7.12.Решить уравнение
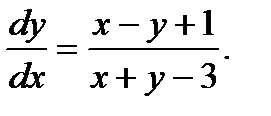 (7.42)
(7.42)
Решение.Поскольку 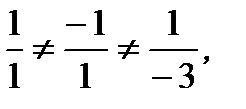 то прямые
то прямые 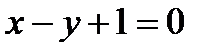 и
и 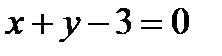 пересекаются. Решая систему линейных уравнений с двумя неизвестными
пересекаются. Решая систему линейных уравнений с двумя неизвестными
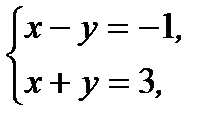 (7.43)
(7.43)
находим координаты точки пересечения прямых в виде 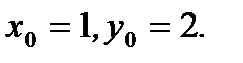 После введения новых переменных
После введения новых переменных 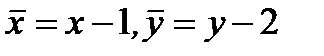 с учетом того, что
с учетом того, что
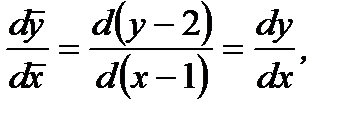 (7.44)
(7.44)
исходное уравнение (7.42) преобразуется к виду
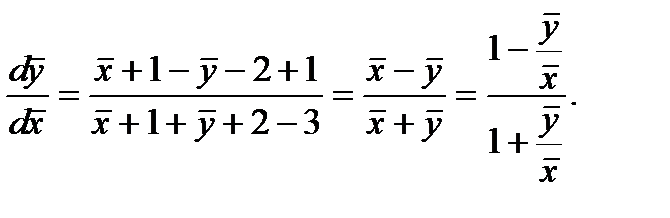 (7.45)
(7.45)
Последнее уравнение представляет собой однородное уравнение, которое подстановкой 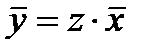 сводится к уравнению с разделяющимися переменными вида
сводится к уравнению с разделяющимися переменными вида
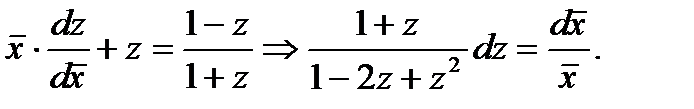 (7.46)
(7.46)
После интегрирования (7.46) получим
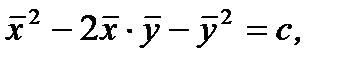 (7.47)
(7.47)
где 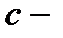 произвольная постоянная. Переходя в (7.47) к переменным
произвольная постоянная. Переходя в (7.47) к переменным 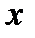 и
и 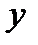 , получим общее решение исходного уравнения
, получим общее решение исходного уравнения
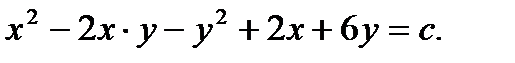 (7.48)
(7.48)
Ответ: 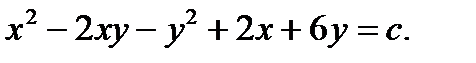
Дата добавления: 2018-11-25; просмотров: 707;
