Уравнения с разделяющимися переменными.
Уравнение вида
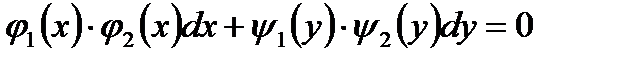 (7.9)
(7.9)
называется уравнением с разделяющимися переменными. В этом уравнении легко разделить переменные, если обе части уравнения разделить на 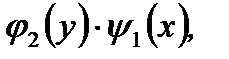 предполагая при этом, что
предполагая при этом, что 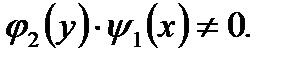 Итак имеем
Итак имеем
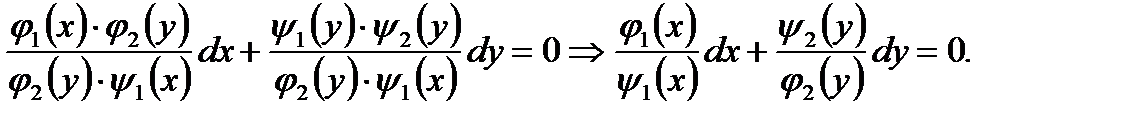 (7.10)
(7.10)
Заметим, что деление обеих частей уравнения (7.9) на 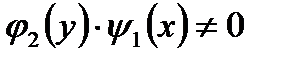 может привести к потере частных решений этого уравнения, обращающих в нуль выражение
может привести к потере частных решений этого уравнения, обращающих в нуль выражение 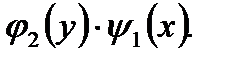 Поэтому, получив общий интеграл уравнения (7.9), следует проверить, содержит ли он упомянутые частные решения при некоторых значениях
Поэтому, получив общий интеграл уравнения (7.9), следует проверить, содержит ли он упомянутые частные решения при некоторых значениях 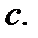 Если нет, то эти решения являются особыми решениями исходного дифференциального уравнения. Отметим также, что в процессе разделения переменных в уравнениях с разделяющимися переменными возможно появление и лишних решений, обращающих в нуль множитель
Если нет, то эти решения являются особыми решениями исходного дифференциального уравнения. Отметим также, что в процессе разделения переменных в уравнениях с разделяющимися переменными возможно появление и лишних решений, обращающих в нуль множитель 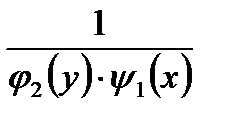 (в этом случае или
(в этом случае или 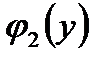 или
или 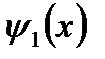 – разрывные функции).
– разрывные функции).
Пример 7.6.Решить уравнение
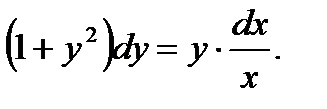 (7.11)
(7.11)
Решение.Разделив обе части уравнения на 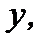 считая, что
считая, что 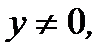 получим уравнение с разделенными переменными
получим уравнение с разделенными переменными
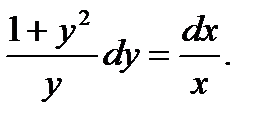 (7.12)
(7.12)
Интегрирование последнего приводит к выражению
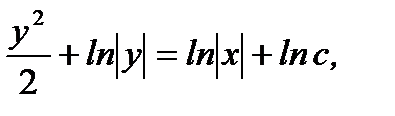 (7.13)
(7.13)
где 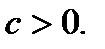 Потенцируя (7.13), получим
Потенцируя (7.13), получим
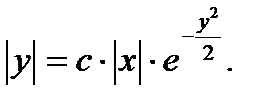 (7.14)
(7.14)
Можно показать, что если теперь  считать произвольной постоянной, включая
считать произвольной постоянной, включая 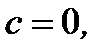 то знаки модулей слева и справа в (7.14) можно убрать. Итак, общее решение исходного уравнения имеет вид
то знаки модулей слева и справа в (7.14) можно убрать. Итак, общее решение исходного уравнения имеет вид
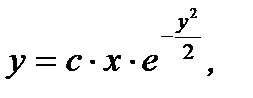 (7.15)
(7.15)
где –  произвольная постоянная.
произвольная постоянная.
Заметим, что решение 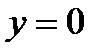 исходного уравнения получается из полученного общего решения (7.15) при
исходного уравнения получается из полученного общего решения (7.15) при 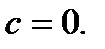
Ответ: 
Пример 7.7.Полные издержки 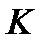 есть функция объема производства
есть функция объема производства 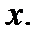 Известно, что предельные издержки равны средним издержкам. Найти закон изменения
Известно, что предельные издержки равны средним издержкам. Найти закон изменения 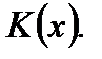
Решение.По условию задачи имеем
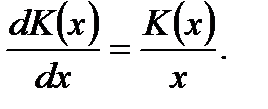 (7.16)
(7.16)
Уравнение (7.16) является дифференциальным уравнением первого порядка с разделяющимися переменными. Разделяя переменные в (7.16), получим
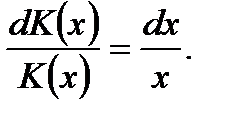 (7.17)
(7.17)
Интегрирование уравнения (7.17) с разделенными переменными приводит к следующему общему решению
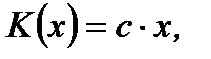 (7.18)
(7.18)
где 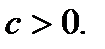 (7.18) показывает, что когда предельные издержки равны средним издержкам, то издержки в зависимости от объема производства меняются по линейному закону.
(7.18) показывает, что когда предельные издержки равны средним издержкам, то издержки в зависимости от объема производства меняются по линейному закону.
Ответ: 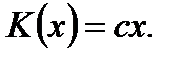
Пример 7.8.Решить задачу Коши
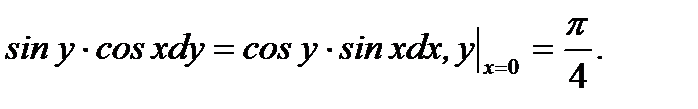 (7.19)
(7.19)
Решение.Уравнение (7.19) является уравнением с разделяющимися переменными. Разделим обе части уравнения на 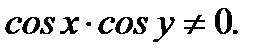 В результате получим уравнение с разделенными переменными
В результате получим уравнение с разделенными переменными
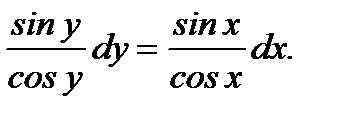 (7.20)
(7.20)
Интегрируя (7.20), получим
 (7.21)
(7.21)
где  произвольная постоянная, не равная нулю. Частное решение получим, пользуясь начальным условием Коши
произвольная постоянная, не равная нулю. Частное решение получим, пользуясь начальным условием Коши 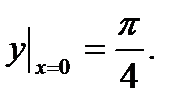 Итак, имеем
Итак, имеем
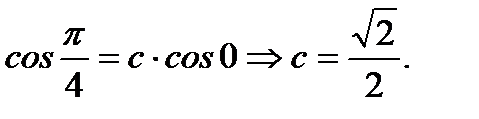 (7.22)
(7.22)
Тогда частное решение имеет вид
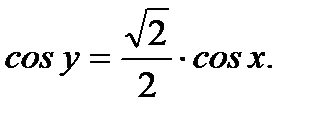 (7.23)
(7.23)
Отметим, что к уравнениям с разделяющимися переменными приводятся уравнения вида
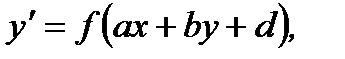 (7.24)
(7.24)
где 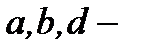 действительные постоянные, подстановкой
действительные постоянные, подстановкой
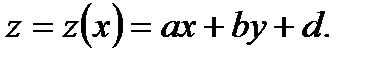 (7.25)
(7.25)
Пример 7.9.Решить уравнение
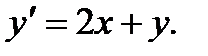 (7.26)
(7.26)
Решение.Введем новую переменную 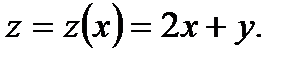 Тогда
Тогда 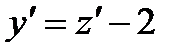 и исходное уравнение преобразуется к виду
и исходное уравнение преобразуется к виду
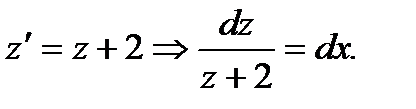 (7.27)
(7.27)
Интегрируя последнее и переходя к переменной 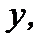 получим общее решение уравнения (7.26) в виде
получим общее решение уравнения (7.26) в виде
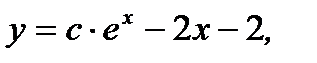 (7.28)
(7.28)
где 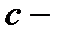 произвольная постоянная.
произвольная постоянная.
Ответ: 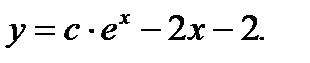
Дата добавления: 2018-11-25; просмотров: 391;
