Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Общий вид указанных уравнений следующий:

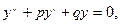
где p и q – постоянные коэффициенты.

Алгоритм решения линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами представлен в таблице № 2.

Таблица №2. Решение линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами

Дифференциальное уравнение
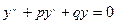
Характеристическое уравнение
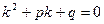
Дискриминант	D > 0	D = 0	D < 0
Корни характеристического уравнения
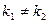
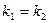
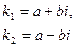
Множества решений

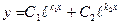
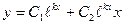
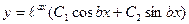
Рассмотрим решение подобных уравнений на конкретных примерах.

Решить уравнение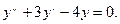

Решение. Составляем характеристическое уравнение:

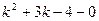
и находим его корни:

k₁ = -4, k₂ = 1.

Общее решение запишется так:

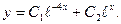
Решить уравнение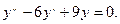

Решение. Составляем характеристическое уравнение:

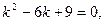
корни которого

к₁ = к₂ = к = 3.

Общее решение запишется так:

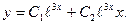
Решить уравнение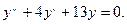

Решение. Составляем характеристическое уравнение:

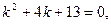
корни этого уравнения

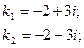
то есть корни мнимые, а = -2, b = 3.

Общее решение будет:

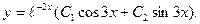
Вопросы для повторения

1 Какое уравнение называется дифференциальным?

2 Назовите виды дифференциальных уравнений.

3 Рассказать алгоритмы решения всех названных в теоретической части работы уравнений.