Говорят, что уравнение

F(x, y) = 0 (2)

неявно задаёт функцию y = f(x) в интервале (a, b), если для любого 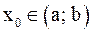уравнение F(x₀; y)=0 имеет единственное решение y₀ = f(x₀).

Для нахождения производной функции 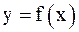, заданной неявно уравнением (2), следует продифференцировать обе части равенства (2), считая 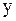функцией от 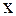; затем полученное уравнение, в которое будут входить x, y и 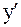, следует разрешить относительно .

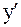Для нахождения 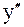равенство (2) дифференцируется дважды, в результате чего получается уравнение, содержащее x, y, 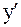, , 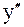которое следует разрешить относительно 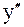, затем вместо 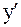подставить функцию от x и y, найденную указанным выше способом.

Пример 6.Найти значения 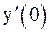, , 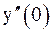если функция y задана неявно уравнением

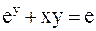. (3)

Решение. Считая y функцией от x, продифференцируем обе части равенства (3): ;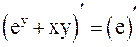

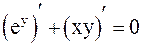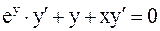; . (4)

Отсюда находим

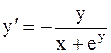; (5)

.

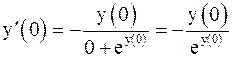Для нахождения y(0) в равенстве (3) положим x = 0:

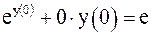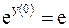; ; y(0) = 1.

Таким образом,

.

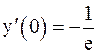Найдём 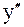, для чего продифференцируем равенство (4):

;

;

.

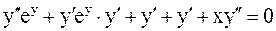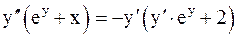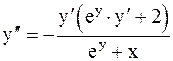Подставив в последнем равенстве вместо 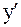выражение (5), получим

,

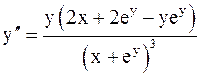откуда находим

.

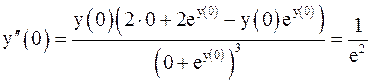Если функция y = y(x) задана параметрическими уравнениями

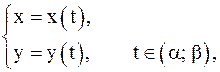
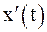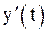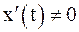то при условии существования производных , и существует производная 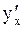и при этом

.

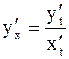Вторая производная 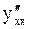находится по формуле

,

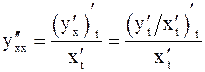или (что то же самое)

.

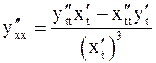Пример 7. Найти 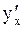, , 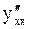если

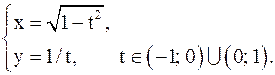
Решение. Имеем:

; ;

;

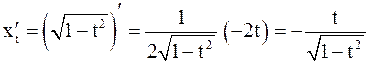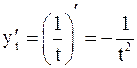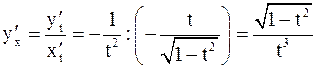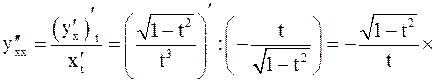
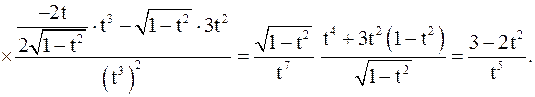
6. Уравнения касательной и нормали

Уравнение касательной к графику функции y = f(x) в точке M(x_0, y₀) имеет вид

,

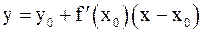а уравнение нормали в той же точке ,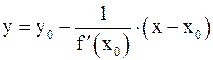

где y₀ = f (x₀).

Пример 8. Найти площадь треугольника, образованного прямой y = y₀ +1, касательной и нормалью, проведёнными к графику

функции y = x³ + 2x² – x + 1 в точке с абсциссой x₀ = 1 и ординатой y₀ .

Решение. Найдём ординату y₀ точки касания и :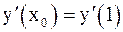

;

; .

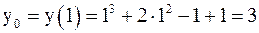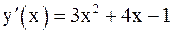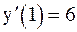Уравнением касательной является y = 3 + 6(x – 1) или 6x – y – 3 = 0. Уравнение нормали имеет вид 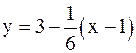или x + 6y – 19 = 0. Найдём координаты точек А и В (см. рисунок) прямой .

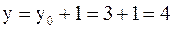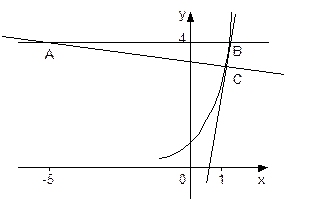
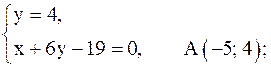
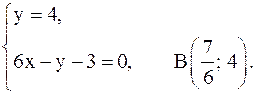
Вычислим длины катетов АС и ВС прямоугольного треугольника АВС:

,

.

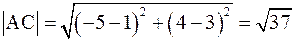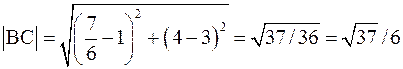По этим данным найдём искомую площадь

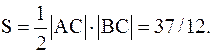
7. Дифференциал первого порядка

Придадим аргументу x в точке x₀ приращение 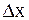, функция y = f(x) получит приращение 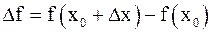. Если существует число А, такое что

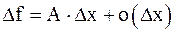, (6)

то говорят, что f(x) дифференцируемая в точке x₀; линейная часть 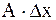приращения функции называется дифференциалом функции в точке x₀ и обозначается 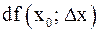или 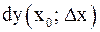(или просто df , dy). Если x – независимое переменное (т.е. не зависит от других переменных), то полагают .

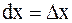Теорема 2. Функция f(x) дифференцируема в точке x₀ в том и только в том случае, если f(x) имеет производную в этой точке. При этом .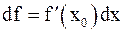

Если в равенстве (6) отбросить бесконечно малую величину 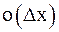, то получим приближённое равенство

,

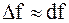которое применяется для нахождения приближённого значения функции.

8. Дифференциалы высших порядков. Формула Тейлора

Дифференциалом второго порядка d²f(x) функции 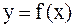называется дифференциал от дифференциала 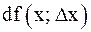, где 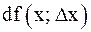рассматривается как функция от x: d²f = d(df). Дифференциалом третьего порядка d³f называется дифференциал от второго дифференциала: d³f = d(d²f) и т.д.

Если переменная x является независимой, то d²x = d³x = … = 0. В этом случае 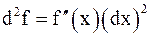, ,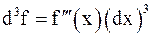..., ,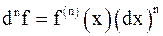… Для краткости вместо (dx)ⁿ принято писать dxⁿ; с учётом этого .

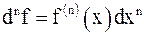Если функция f(x) определена в некоторой окрестности точки x₀ и в этой окрестности имеет производные до (n+1) -го порядка включительно (т.е. дифференцируема (n+1) раз), то справедлива формула Тейлора

,

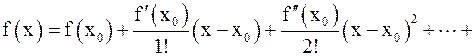
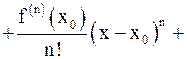
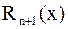где R_n+1 (x) – остаточный член, являющийся бесконечно малой величиной при x ® x₀. Остаточный член обычно записывают в виде

,

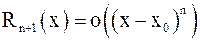в форме Пеано или в форме Лагранжа

,

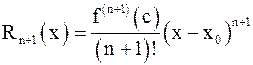где с – некоторое число между x₀ и x. Формула Тейлора допускает и другую запись через дифференциалы

.

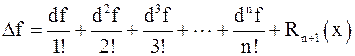Формулу Тейлора применяют для приближенных вычислений.