Показательные неравенства.
1º. Неравенство, содержащее переменную в показателе степени, называется показательным неравенством.
2º. Решение показательных неравенств вида 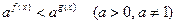 основано на следующих утверждениях:
основано на следующих утверждениях:
если 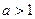 , то неравенство
, то неравенство  равносильно
равносильно 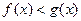 ;
;
если 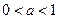 , то неравенство
, то неравенство  равносильно
равносильно 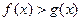 .
.
При решении показательных неравенств используют те же приемы, что и при решении показательных уравнений.
Пример 26. Решить неравенство  (методом перехода к одному основанию).
(методом перехода к одному основанию).
Решение: Так как 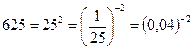 , то заданное неравенство можно записать в виде:
, то заданное неравенство можно записать в виде: 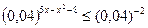 . Так как
. Так как 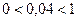 , то данное неравенство равносильно неравенству
, то данное неравенство равносильно неравенству  .
.
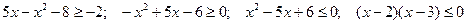 .
.
Решив последнее неравенство, получим 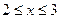 .
.
Ответ: 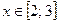 .
.
Пример 27. Решить неравенство: 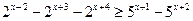 (методом вынесения общего множителя за скобки).
(методом вынесения общего множителя за скобки).
Решение: Вынесем за скобки в левой части неравенства 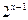 , в правой части неравенства
, в правой части неравенства 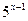 и разделим обе части неравенства на (-2), поменяв знак неравенства на противоположный:
и разделим обе части неравенства на (-2), поменяв знак неравенства на противоположный:
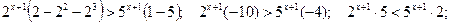
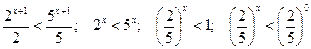 .
.
Так как  , то при переходе к неравенству показателей знак неравенства опять меняется на противоположный. Получаем
, то при переходе к неравенству показателей знак неравенства опять меняется на противоположный. Получаем  . Таким образом, множество всех решений данного неравенства есть интервал
. Таким образом, множество всех решений данного неравенства есть интервал 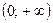 .
.
Ответ: 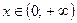 .
.
Пример 28. Решить неравенство 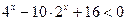 (методом введения новой переменной).
(методом введения новой переменной).
Решение: Пусть 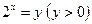 . Тогда данное неравенство примет вид:
. Тогда данное неравенство примет вид: 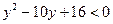 или
или 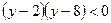 , решением которого является интервал
, решением которого является интервал 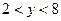 .
.
Отсюда 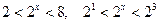 . Поскольку функция
. Поскольку функция 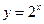 возрастает, то
возрастает, то 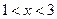 .
.
Ответ: 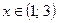 .
.
Дата добавления: 2017-09-19; просмотров: 277;
