Дидактический материал.
1. В треугольнике ABC длины сторон AB и AC соответственно равны 4 и 6, а синус угла BAC равен 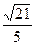 . Тогда сторона CB (CB>8) равна:
. Тогда сторона CB (CB>8) равна:
1) 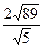 2)
2) 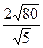 3)
3) 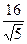 4)
4) 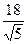 5)
5) 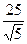 .
.
2. В равнобедренном треугольнике основание равно 18, а боковая сторона в 1,25 больше высоты. Тогда площадь треугольника равна:
1) 216 2) 108 3) 144 4) 121 5) 110.
3. В треугольнике сторона, равная 12, расположена против угла 30º. Тогда радиус описанной около этого треугольника окружности равен:
1) 24 2) 14 3) 12 4) 8 5) 15.
4. Около прямоугольника с меньшей стороной, равной 46, и углом между диагоналями, равным 60º, описана окружность. Тогда площадь круга равна:
1) 1058π 2) 1600π 3) 2116π 4) 1024π 5) 625π.
5. В ромб вписана окружность радиуса 2. Определить площадь ромба, если его острый угол равен 60º.
1) 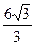 2)
2) 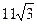 3)
3) 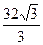 4)
4) 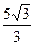 5) 16
5) 16
6. Даны стороны треугольника 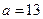 см,
см, 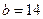 см,
см, 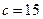 см. Тогда радиус описанной около него окружности равен:
см. Тогда радиус описанной около него окружности равен:
1) 64 2) 8 3) 7 4) 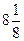 5)
5) 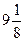
7. В треугольник вписан круг радиуса 4 см. Одна из сторон треугольника разделена точкой касания на части, равные 6 см и 8 см. Тогда длины двух других сторон равны:
1) 13 и 12 2) 12 и 8 3) 13 и 15 4) 11 и 9 5) 10 и 6.
8. Внутри круга, радиус которого равен 13 см, дана точка М, отделенная от центра круга на 5 см. через точку М проведена хорда 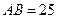 см. Тогда длины отрезков, на которые хорда AB делится точкой М, равны:
см. Тогда длины отрезков, на которые хорда AB делится точкой М, равны:
1) 9 и 16 2) 8 и 17 3) 4 и 21 4) 5 и 20 5) 6 и 19
9. Длины катетов прямоугольного треугольника равны 2 и 3. Тогда длина биссектрисы прямого угла этого треугольника равна:
1) 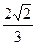 2)
2) 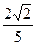 3)
3) 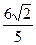 4)
4) 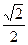 5)
5) 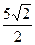
10. Длины оснований трапеции относятся как 7:3 и различаются на 8. Тогда длина средней линии трапеции равна:
1) 6 2) 10 3) 12 4) 8 5) 5.
11. Найти диагональ и боковую сторону равнобедренной трапеции с основаниями 20 см и 12 см, если известно, что центр описанной окружности лежит на большем основании.
1) 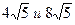 2)
2) 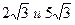 3)
3) 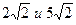 4)
4) 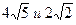
5) 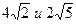
12. Площадь квадрата, вписанного в правильный треугольник со стороной a, равна:
1) 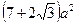 2)
2) 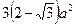 3)
3) 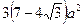 4)
4) 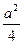 5)
5) 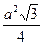 .
.
13. Площадь трапеции, параллельные стороны которой равны 16 и 44, а непараллельные – 17 и 25, равна:
1) 420 2) 430 3) 440 4) 450 5) 460
14. Медиана, проведенная к боковой стороне равнобедренного треугольника, делит его периметр на две части, длины которых равны 30 и 12 соответственно. Определить длину основания треугольника.
1) 1 2) 1,5 3) 2 4) 2,5 5) 3.
15. Сторона ромба равна 16, острый угол равен 30º. Определить радиус вписанного круга.
1) 3 2) 3,5 3) 4 4) 4,5 5) 5.
16. Круг описан около прямоугольного треугольника, один из катетов которого равен 6 см, а угол, лежащий против этого катета, равен 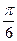 . Тогда площадь круга равна:
. Тогда площадь круга равна:
1) 6π см2 2) 9π см2 3) 36π см2 4) 144π см2 5) 24π см2
Дата добавления: 2017-09-19; просмотров: 255;
