Стереометрия. Круглые тела, тела вращения.

1º. Прямым круговым цилиндром (или просто цилиндром) называется тело, образованное вращением прямоугольника вокруг оси, содержащей его сторону. Разверткой боковой поверхности цилиндра является прямоугольник, стороны которого равны длине окружности основания цилиндра и его высоте.

Если обозначить за R – радиус основания, H – его высоту, l – образующую, S_бок – площадь боковой поверхности, V – объем, то:

; .

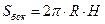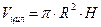2º. Прямым круговым конусом (или просто конусом) называется тело, образованное вращением прямоугольного треугольника вокруг оси, содержащей его катет. Развертка боковой поверхности конуса является круговым сектором.

Если обозначить за R – радиус основания, H – его высоту, l – образующую, S_бок – площадь боковой поверхности, V – объем, то:

; .

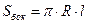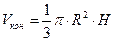3º. Сферой называется множество точек пространства, находящихся на данном расстоянии от данной точки, называемой центром этой сферы.

Шаром называется множество точек пространства, расстояние от каждой из которых до данной точки (центра шара) не превосходит данного расстояния R (радиуса шара).

Если обозначить за R – радиус шара (сферы), S – площадь сферической поверхности, V – объем, то:

; .

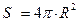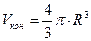4º. Шаровой сегмент – часть шара, отсекаемая от него плоскостью.

Если обозначить за R – радиус шара, h – высоту сегмента, S – площадь сферической поверхности сегмента, V – объем, то:

; .

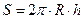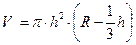5º. Шаровой сектор – часть шара, ограниченная конической поверхностью с вершиной в центре шара и поверхностью шара.

Если обозначить за R – радиус шара, h – высоту сегмента, V – объем, то:

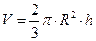
Пример 52. Площадь осевого сечения прямого кругового цилиндра равна 24. Найти площадь его боковой поверхности.

1) 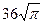2) 24π 3) 72 4) 68 5)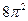

Решение.

Указание. При решении задач на «круглые тела» можно ограничиться изображением осевого сечения тела.

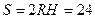Пусть прямоугольник ABCD – осевое сечение данного цилиндра. Тогда по условию задачи его площадь равна: . Но .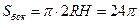

Ответ: 24π (№2 – правильный ответ).

Пример 53. Образующая прямого кругового конуса равна 4 и наклонена к плоскости основания под углом 30º. Найти объем конуса.

1) 8π 2) 6π 3) 4π 4) 10π 5) 12π.

Решение.

Пусть равнобедренный треугольник ABC – осевое сечение данного конуса. По условию задачи образующая BC конуса равна 4, т.е. 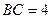, кроме того, 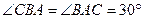и OB – радиус основания конуса. Обозначим: 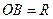. Тогда из ΔOBC найдем: 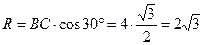, высота конуса 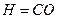равна в ΔOBC половине гипотенузы 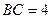, т.е. 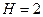. По формуле объема конуса:

.

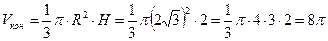Ответ: 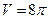(№1 – правильный ответ).