Осесимметричные оболочки вращения. Их основные нагрузки и напряжения. Уравнения Лапласа.

Оболочка вращения называется осесимметричнойесли она нагружена: силами распределенными симметрично вокруг оси; краевыми силами, распределенными равномерно по параллельному кругу; краевыми моментами, равномерно распределенными по параллельному кругу.

Самым общим случаем нагружения каждой точки поперечного сечения осесимметричных оболочек вращения действуют следующие удельные нагрузки, распределенные равномерно по толщине стенки оболочки:

1. S – меридиональная сила – это сила приходящаяся на единицу длины параллельного круга и растягивающая элемент в меридиональном направлении.

2.Т – кольцевая сила – это сила приходящаяся на единицу длины меридиана и стремящаяся растянуть элемент в направлении параллельного круга.

3.М – меридиональный момент – это момент, приходящийся на единицу длины параллельного круга и стремящийся изменить кривизну элемента в направлении меридиана.

4.К – кольцевой момент – изгибающий момент, приходящийся на единицу длины меридиана и стремящийся изменить кривизну элемента в направлении параллельном меридиана.

5.Q – поперечная сила – это сила, приходящаяся на единицу длины меридиана.

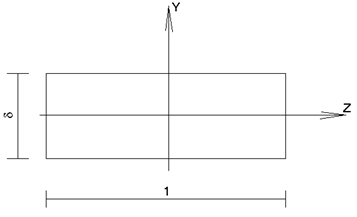
Напряжения, возникающие от действия удельных нагрузок определяются если предположить, что грани элемента к которому приложена нагрузка имеют форму прямоугольника с основанием равным 1 и высотой равной толщине стенки аппарата.

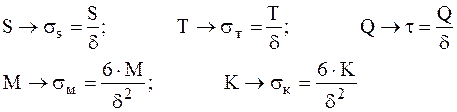
Согласно принципа суперпозиции (независимости действия сил) одноименные силы суммируются

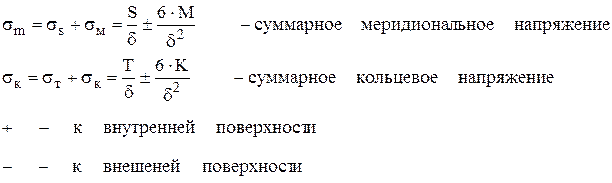Вывод: таким образом самым общим случаем нагружения ассиметричные оболочки вращения испытывают действия трех напряжений: меридиональное, кольцевое и касательное, которые учитывают действие всех внутренних удельных нагрузок.

Теория расчета оболочек, которая учитывает действие всех внутренних удельных нагрузок – моментная теория расчета.

На практике при расчете тонкостенных оболочек вращения, находящихся под действием равномерно распределенного давления поперечную силу и изгибающие моменты не учитывают. Такую теорию расчета называют безмоментной теорией расчета оболочек.

Основным уравнением безмоментной теории расчета на прочность ассиметричных оболочек вращения нагруженных давлением является уравнение Лапласа.

,

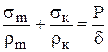Р – внутреннее давление;

δ – толщина стенки оболочки.

Лекция №4.