Теории прочности, применяемые при расчетах М и АХП.
Машины и аппараты с тонкой стенкой рассчитываются по третьей теории прочности.
Это теория максимальных касательных напряжений, согласно которой разрушение элементов конструкции наступает тогда, когда касательные напряжения в ней достигнут опасного значения.
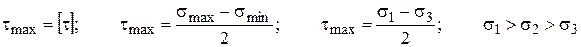
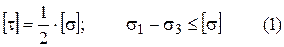
Т. к. элементы конструкции тонкостенных аппаратов находятся в плоском напряженном состоянии, а нормальные напряжения вычисляются
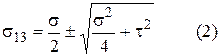
Подставим (1) в (2):
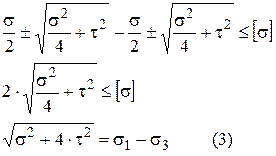
σ – нормальные напряжения, возникающие в каждой точке поперечного сечения элементов конструкции, вызванное действием изгибающей нагрузки.
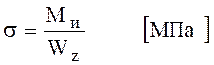 ,
,
где 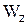 – осевой момент сопротивления.
– осевой момент сопротивления.
Для вала 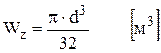
τ – касательные напряжения, возникающие в каждой точке поперечного сечения от действия крутящего момента.
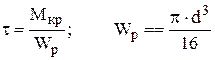 ,
,
где Wр – полярный момент сопротивления.
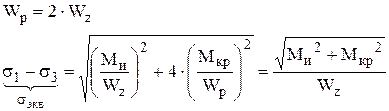
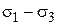 – эквивалентные напряжения, вычисленные по третьей теории прочности;
– эквивалентные напряжения, вычисленные по третьей теории прочности;
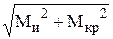 – эквивалентные моменты, вычисленные по третьей теории прочности.
– эквивалентные моменты, вычисленные по третьей теории прочности.
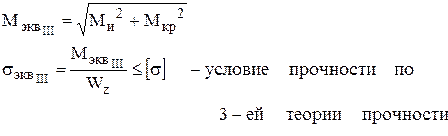
Тонкостенные оболочки. Оболочки вращения. Основные понятия и определения.
Машины и аппараты называются тонкостеннымиесли отношение исполнительной толщины стенки к внутреннему диаметру не превышает 0,1 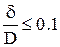 .
.
Оболочкойназывается тело ограниченное двумя криволинейными поверхностями, расположенными на близком расстоянии друг от друга.
В зависимости от формы срединой поверхности (это геометрическое место точек, равно удаленное от двух криволинейных поверхностей) оболочки подразделяются на: цилиндрические, сферические, конические.
Если срединная поверхность плоская кривая – это пластина.
Большинство форм элементов машин и аппаратов являются оболочками вращения, срединную поверхность, которой можно получить при вращении любой плоской кривой вокруг некоторой оси.
Расчетная схема:(методичка стр. 19, рис. 2.1.)
Опр. 1:При вращении любой точки, принадлежащей плоской кривой вокруг оси, эта точка описывает окружность радиусом r, называемая параллельнымкругом.
Опр. 2:Кривая пересечения срединой поверхности плоскостью, проходящей через ось, называется меридианом.
Опр. 3:Радиус кривизны срединой поверхности в направлении меридиана называется первымглавнымрадиусомкривизны (ρm).
Опр. 4:Радиус кривизны срединой поверхности в направлении перпендикулярном меридиану называется вторымглавнымрадиусомкривизны (ρк).
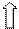 Для цилиндра
Для цилиндра 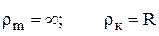
Для шара 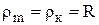
Дата добавления: 2019-02-07; просмотров: 609;
