Метод неопределённых коэффициентов.
Если правая часть неоднородного уравнения имеет вид 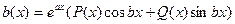
то частное решение существует в виде 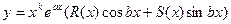 ,
,
где 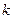 это кратность числа
это кратность числа 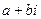 в качестве характеристического корня. Если оно не является корнем, то
в качестве характеристического корня. Если оно не является корнем, то 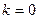 . Тогда домножение происходит на
. Тогда домножение происходит на 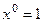 , то есть фактически, не происходит.
, то есть фактически, не происходит.
Если в правой части нет тригонометрических функций, то всегда может автоматически считаться, что 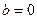 , то есть
, то есть
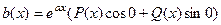 =
= 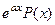 .
.
Если отсутствует многочлен, а просто есть экспонента, то можем считать, что многочлен просто равен константе 1, то есть формально он всё равно есть, нулевой степени. Тогда в структуре частного решения записывается «произвольный» многочлен 0 степени, то есть константа А.
Для 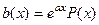 частное решение в виде
частное решение в виде 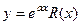 , если
, если 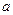 не является характеристическим корнем, либо
не является характеристическим корнем, либо 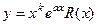 , если
, если 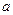 совпадает с каким-то характеристическим корнем кратности
совпадает с каким-то характеристическим корнем кратности 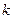 .
.
Покажем на примере того же уравнения, которое только что решали методом Лагранжа.
Пример. Решить уравнение 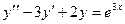 .
.
Шаг 1. Решается однородное. Характеристическое уравнение 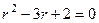 . Его корни равны 1 и 2, общее решение однородного
. Его корни равны 1 и 2, общее решение однородного 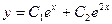 .
.
Шаг 2. Решение неоднородного. Правая часть 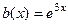 , число 3 не совпадает ни с каким характеристическим корнем левой части, так как там корни 1 и 2. Поэтому
, число 3 не совпадает ни с каким характеристическим корнем левой части, так как там корни 1 и 2. Поэтому 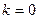 , и по правой части
, и по правой части 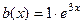 надо записать структуру частного решения:
надо записать структуру частного решения: 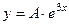 .
.
Найдём производные до второго порядка от 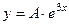 и подставим их в неоднородное уравнение.
и подставим их в неоднородное уравнение.
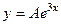

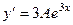

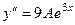 .
.
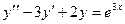

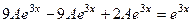

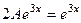

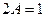

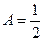 . Таким образом, частное решение неоднородного:
. Таким образом, частное решение неоднородного:
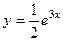 , а общее решение неоднородного:
, а общее решение неоднородного: 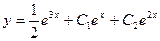 .
.
Дата добавления: 2017-05-18; просмотров: 485;
