Общее, частное решение. Задача Коши.

Как мы только что увидели, решений бесконечно много, и они заполняют всю плоскость. Здесь константа С может участвовать в выражении совершенно по-другому, чем в задачах на интегралы: там первообразные отличаются на константу, то есть получаются одна из другой параллельным переносом. Здесь C может быть и множителем или участвовать в уравнении как-то иначе.

Через каждую конкретную точку плоскости проходит одна кривая из этого семейства кривых. Если задать точку 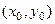и наложить условие, что кривая проходит через неё, то есть 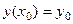, то можно определить конкретное значение параметра 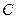, и одну кривую из бесконечного множества. Это дополнительное условие называется условием Коши. Чтобы найти эту одну кривую, надо подставить 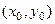в общее решение, и там останется одна неизвестная 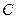. 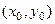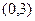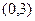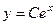Например, если = , то есть кривая проходит через точку , то запишется в виде 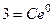, тогда 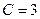. Функция 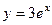называется частным решением.

Кстати, движение в физике задаётся с помощью уравнений со 2-й производной (это ускорение), там в общем решении две константы, поэтому как раз и требуется 2 условия (начальная координата и начальная скорость), чтобы определить конкретную траекторию.

Поле направлений.

Если задано дифференциальное уравнение 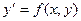, то это означает, что в каждой точке некоторой области D задано направление касательной, т.е. под каким углом наклона там пройдёт кривая. Ведь 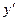это тангенс угла наклона производной, и он дан для каждой точки, а именно равен 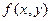. Возникает так называемое «поле направлений». Иногда даже зрительно можно заранее предположить, какие кривые являются решениями дифф. уравнения. Увидим это на следующем примере.

Пример. Решить дифференциальное уравнение .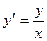

Заметим, что тангенс угла наклона касательной для любого решения здесь равен 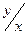, то есть касательные направлены радиально от центра.

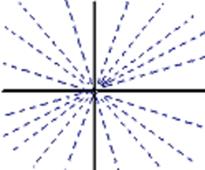
Можно предположить, что решения это прямые вида 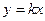. А теперь решим задачу аналитически.

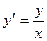
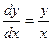
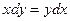
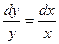
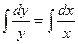
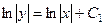. Кстати, любую константу можно задать в виде 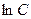, так как область значений логарифма 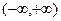. Для удобства сразу запишем 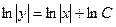, чтобы логарифмировать это выражение. Впрочем, это не обязательно делать именно так, 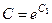можно преобразовать и позже.

Далее, .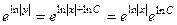

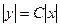В итоге, общее решение .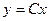

Проверка. 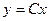, , 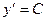подставим в уравнение 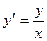получим 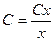. Действительно, верно.