Пункт 3. Линейные уравнения.

Уравнение вида 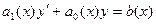называется линейным.

Если 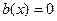, то оно называется линейным однородным.

При этом, 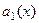не может быть тождественно равно 0, иначе вообще нет слагаемого с производной 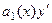, то есть уравнение не являлось бы дифференциальным. Но тогда можно поделить всё уравнение на 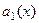и свести к виду .

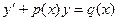Линейные однородные уравнения фактически являются уравнениями с разделяющимися переменными. Действительно, ,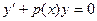

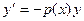
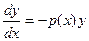
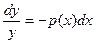
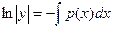где 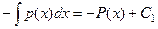первообразная, с точностью до константы. В итоге, 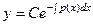, то есть общее решение линейного однородного уравнения имеет вид: константа, умноженная на экспоненту в степени первообразной от коэффициента 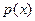, взятую с другим знаком.

Пример. Решить уравнение .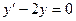

.

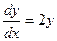
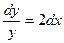
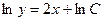
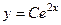Мы видим коэффициент 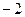, её первообразная 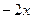, соответственно в ответе есть .

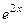Пример. Решить уравнение .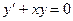

Можно рассмотреть 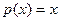, первообразная равна ,

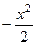тогда = .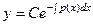

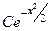Впрочем, можно его решить и просто как уравнение с разделяющимися переменными:

.

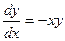
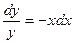
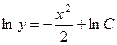
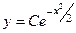Линейные неоднородные уравнения. Метод Лагранжа (другое название: метод вариации произвольной постоянной).

Предположим, что на месте C некоторая неизвестная функция, и ищем решение в виде: .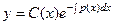

Тогда .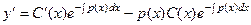

Подставим эти 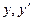в неоднородное уравнение .

+ .

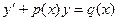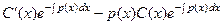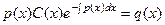Два слагаемых получились одинаковые, и они сокращаются, осталось:

= .

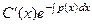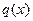Отсюда можно выразить . .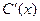

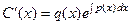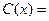
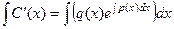что состоит в итоге из 2 слагаемых:

первообразной от 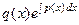и константы 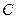. Поэтому решение однородного обязательно окажется отдельным слагаемым в общем решении неоднородного.

.

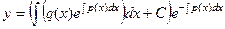В конкретных примерах, это выглядит менее громоздко:

Пример. Решить линейное уравнение .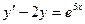

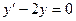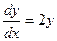
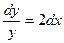
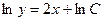
1 шаг. Решаем соответствующее однородное уравнение. . 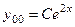- общее решение однородного.

2 шаг. Методом Лагранжа решаем неоднородное.

Ищем решение в виде: 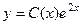. Ищем производную:

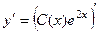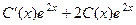= . Всё это подставим в неоднородное:

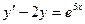
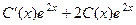
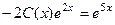
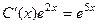, тогда .

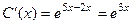Тогда = .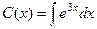

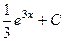Теперь подставим это в 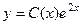, получается

= .

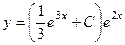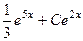Общее решение неоднородного состоит из двух слагаемых: частное решение неоднородного (его мы и искали на 2-м шаге методом Лагранжа) и общее решение однородного, которое нашли на 1-м шаге, и оно воспроизвелось само в конце 2-го шага. Это происходит из-за того, что 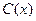всегда ищется с помощью её производной, а значит, в ней присутствует слагаемое .

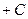Проверка. Можно подставить частное решение неоднородного, и это слагаемое само по себе тоже является решением:

Выполняется ли ?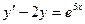

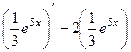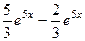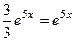= = . Верно.