Системы дифференциальных уравнений.
Ознакомительно изучим системы дифференциальных уравнений. Как правило, система из n уравнений сводится к уравнению порядка n, поэтому часто для решения систем дифф. уравнений достаточно уметь решать уравнения порядка n. Однако здесь есть и матричный метод решения, не предполагающий сведение системы к уравнению.
Если есть несколько равенств, выражающих производные от различных функций через сами эти функции, например,
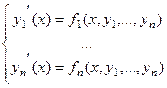
то говорят, что задана система дифференциальных уравнений.
Если рассматривать столбец, состоящий из функций 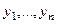 как векторную функцию, то вид записи системы похож на вид уравнения 1 порядка:
как векторную функцию, то вид записи системы похож на вид уравнения 1 порядка: 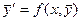 .
.
Как правило, при размерности пространства 3, в физических задачах, переменную обозначают 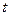 (время), а функции
(время), а функции 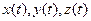 .
.
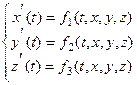
Если все функции 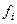 не зависят от
не зависят от 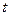 , а выражаются только через
, а выражаются только через 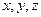 , то система называется автономной.
, то система называется автономной.
Система линейных однородных дифференциальных уравнений:
В 2-мерном случае 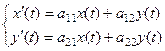
В 3-мерном случае 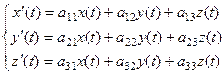
Физический смысл. Вектор, состоящий из производных, это вектор скорости, а выражен он через координаты в момент времени 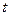 . Получается, что система дифференциальных уравнений задаёт закон движения некоторого потока частиц. К примеру, если в некотором объёме дует ветер, то от того, куда поместить пылинку, зависит траектория её дальнейшего полёта. Если поток не меняется, то траектория не зависит от времени (когда система автономна). Задать координаты в нулевой момент времени
. Получается, что система дифференциальных уравнений задаёт закон движения некоторого потока частиц. К примеру, если в некотором объёме дует ветер, то от того, куда поместить пылинку, зависит траектория её дальнейшего полёта. Если поток не меняется, то траектория не зависит от времени (когда система автономна). Задать координаты в нулевой момент времени 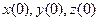 означает задать условия Коши для системы дифференциальных уравнений.
означает задать условия Коши для системы дифференциальных уравнений.
Методы решения. Можно свести систему из двух уравнений 1-го порядка к одному уравнению, но 2-го порядка. Рассмотрим на примере.
Пример. Решить систему дифференциальных уравнений
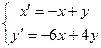
Решение. Выразим из 1-го  , тогда
, тогда  , подставим во 2-е:
, подставим во 2-е: 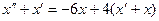 что сводится к
что сводится к 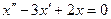 .
.
Это линейное однородное уравнение решается обычным образом, его общее решение 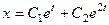 .
.
Тогда 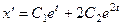 ,
, 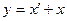 =
= 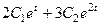 .
.
Итак, общее решение системы:
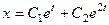 ,
, 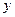 =
= 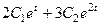
Его можно записать в векторной форме:
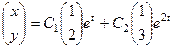

Кстати, векторы (1,2) и (1,3) являются собственными векторами матрицы этой системы, причём они соответствуют собственным числам 1 и 2. Существует и второй способ решения систем: с помощью собственных векторов.
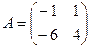 ,
, 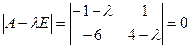

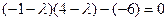

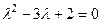

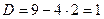
Корни 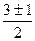 то есть 1 и 2. Ищем собственные векторы:
то есть 1 и 2. Ищем собственные векторы:
При 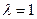 нужно решить систему
нужно решить систему 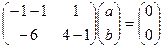 , т.е.
, т.е.
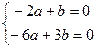 , что даёт вектор (1,2).
, что даёт вектор (1,2).
При 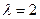 нужно решить систему
нужно решить систему 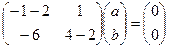 , т.е.
, т.е.
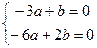 , что даёт вектор (1,3).
, что даёт вектор (1,3).
ФСР состоит из собственных векторов, умноженных на экспоненты в степени собственных чисел.
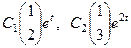 .
.
Дата добавления: 2017-05-18; просмотров: 711;
