Линейные дифференциальные уравнения порядка n.

Уравнение вида 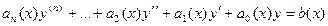называется линейным дифференциальным уравнением порядка n.

Если 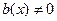то оно называется неоднородным, а если , то однородным: .

Линейное однородное уравнение с постоянными коэффициентами:

.

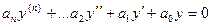Если составить многочлен с теми же коэффициентами, и степенными функциями той же степени, что был на этом же месте порядок производной, то такой многочлен называется характеристическим, а уравнение 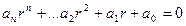- характеристическим уравнением.

Теорема 1. Функция 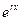является решением линейного однородного дифференциального уравнения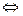 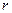есть характеристический корень.

Доказательство. Ищем решение в виде .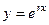

Если 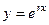, то , , ... .

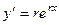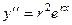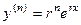Подставим в уравнение .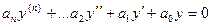

Получим .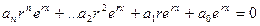

Во всех слагаемых одинаковая экспонента, вынесем её за скобку:

.

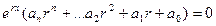Но поскольку 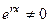, то .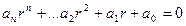

Что и требовалось доказать.

Итак, решениями могут быть не все экспоненты, а лишь некоторые избранные, не более n штук, потому что многочлен степени n имеет не больше n различных корней.

Теорема 2. Линейная комбинация решений линейного однородного дифференциального уравнения тоже является его решением.

Доказательство.

Пусть 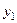и 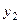- два различных решения уравнения

.

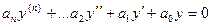То есть, они оба обращают его в тождество:

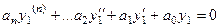и

.

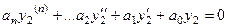Надо доказать, что линейная комбинация 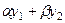тоже подходит в качестве решения. Известно, что для производной, а также и последующих выполняется свойство линейности: 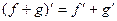, поэтому 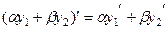, , и т.д.

Тогда, подставляя линейную комбинацию в дифференциальное уравнение, получим:

=

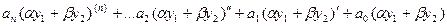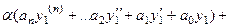
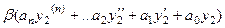
Но ведь в каждой скобке 0, так как каждая из этих функция была решением уравнения. Получается .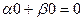

Таким образом, линейная комбинация решений тоже является решением линейного уравнения.

Случай 1. Все характеристические корни действительны и различны.

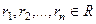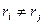, . Тогда возможные решения это n различных экспонент: 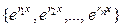. Эта система функций называется «фундаментальная система решений» (ФСР). Но так как по теореме 2, любая линейная комбинация тоже является решением, то все функции вида 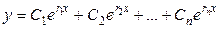тоже решения.

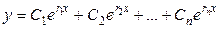называется «общим решением» дифференциального уравнения.

Пример.Решить уравнение .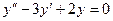

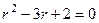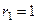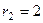Решение. Характеристическое уравнение: , оно сводится к виду , корни , . Тогда решениями могут быть только 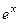и 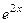. Сделаем проверку для каждой из экспонент. Подставим каждую из них в уравнение.

1) = .

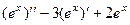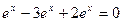2) = .

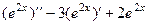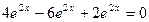Проверка выполнена. Обе экспоненты являются решениями.

При этом никакая третья экспонента не может служить решением этого же уравнения, потому что характеристический многочлен 2-й степени, и он имеет максимум 2 корня.

ФСР состоит из 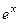и 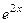. Общее решение: .

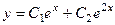Случай 2.Все характеристические корни действительные, но среди них есть кратные.

Если 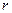есть корень кратности 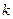, то в системе решений будут присутствовать 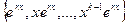, то есть одну и ту же экспоненту 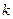раз включать в фундаменатльную систему решений нельзя, иначе фактическое количество функций в ФСР получится меньше, чем n.

Кроме самой экспоненты, нужно взять ещё и с домножением на степенные, по нарастанию степеней до .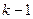

Пример. Решить уравнение .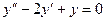

Решение. Характеристическое уравнение: 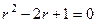, то есть 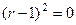, характеристическое корни 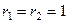. Тогда ФСР: 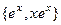, а общее решение: .

Сделаем проверку. Для 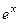очевидно. Проверим .

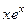, тогда , .

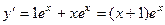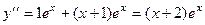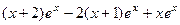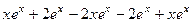= = = = 0.

Случай 3. Не все корни действительны (есть комплексные характеристические корни).

Если корень 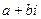(а также при этом и ), то в ФСР, в числе всех прочих, входят две такие функци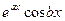и: и .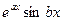

Пример. 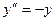, такой пример мы выше решали и другим способом, а теперь рассмотрим это уравнение как линейное. Характеристическое уравнение 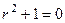, корни , то есть . Решения .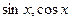

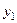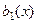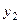Теорема 3.(Теорема о наложении решений). Если - решение линейного неоднородного дифф.уравнения с правой частью , а - решение такого же дифф.уравнения, но с правой частью 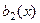, то сумма 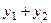является решением уравнения с правой частью .

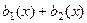Доказательство. Доказывается аналогично теореме 2.

Пусть верно 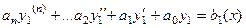и

.

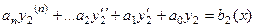Тогда подставим сумму в левую часть: =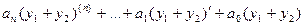

+ = .

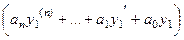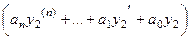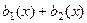Таким образом, если в неоднородном уравнении правая часть состоит из нескольких слагаемых, то можно решить более простые уравнения (для каждого из них отдельно) и сложить решения.

Замечание. Такое же утверждение верно не только для суммы, но и для линейной комбинации. Здесь коэффициенты равны 1 только для простоты и наглядности доказательства.

Следствие 1. Сумма решений линейного неоднородного и соответствующего однородного дифференциального уравнения является решением неоднородного уравнения.

Доказательство. В условиях прошлой теоремы, взять одну правую часть 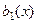, а вторую 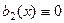. тогда сумма решений 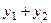является решением уравнения с правой частью .

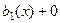Следствие 2. Разность двух различных решений линейного неоднородного дифференциального уравнения является решением соответствующего однородного.

(Слово «соответствующего» здесь означает, что с той же левой частью, что и было неоднородное).

Понятие линейной комбинации, которое рассмотрели выше, здесь обобщено из векторной алгебры (вспомнить системы векторов). Рассмотрим другие обобщения, например, линейной зависимости и независимости системы.

Определение. Система функций 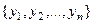называется линейно-независимой, если из равенства 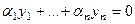следует, что все коэффициенты . Если же это равенство возможно при каком-то наборе коэффициентов (т.е. не все они равны 0), то система называется линейно-зависимой.

Примеры. 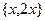ЛЗС. Возьмём коэффициенты 2 и .

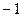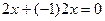. Если в системе есть хотя бы две пропорциональные функции, то системы ЛЗС.

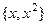ЛНС. Какими бы ни были коэффициенты, получается многочлен 2 степени 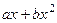, и здесь 0 может получиться, только лишь в том случае, если обнулить все коэффициенты.

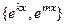ЛНС. Ни одна экспонента одной степени не представляется в виде другой экспоненты, умноженной на коэффициент.

Чтобы выяснить, ЛЗС или ЛНС система векторов, в линейной алгебре применяли определители. Здесь же фактически нет матрицы, так как просто n скалярных функций. Тем не менее, оказывается, что здесь тоже можно достроить до квадратной матрицы, а именно с помощью их производных. Если во 2-й строке записать все их первые производные, в 3-й строке - вторые производные, и так далее, до порядка, с той целью, чтобы получилась именно квадратная матрица, такой определитель называется определителем Вронского.

Рассмотрим определители Вронского в тех примерах, которые были выше.

Система функций .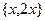

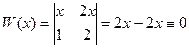
Система функций . .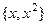

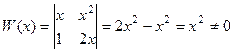Система функций . =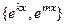

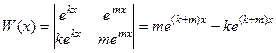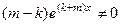, так как числа разные (разность в скобке точно не 0) а экспонента не равна 0.

Как видим на примерах, определитель Вронского для линейно зависимой системы получился тождественно равен 0, а для независимых - нет. На следующей лекции докажем этот факт в общем виде.

ЛЕКЦИЯ № 8. 04.04.2017.

Лемма.Система функций линейно зависима 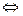хотя бы одна из них является линейной комбинацией остальных.

Доказательствоаналогично тому, что было для векторов. Например, необходимость. Пусть какой-то коэффициент в выражении 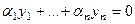отличен от 0. Тогда оставим с одной стороны равенства именно это слагаемое, а затем разделим на этот коэффициент. Например, пусть не равен нулю коэффициент 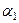. Тогда 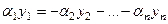, откуда следует .

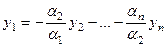Теорема 4.Система функций линейно-зависима .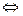

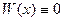Доказательство.

Необходимость.Система функций линейно зависима 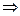верно 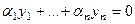при некотором наборе коэффициентов, среди которых есть отличные от 0. Это эквивалентно тому, что одну из функция можно выразить через другие, то есть представить в виде линейной комбинации. Допустим для определённости, что 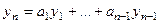. Используем свойство .

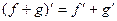Тогда и для её производной верно аналогичное равенство:

.

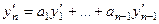Это же верно и для вторых производных, и для каждой из последующих. Но это эквивалентно тому, что в определителе

последний столбец является линейной комбинацией предыдущих столбцов, тогда определитель равен 0 при любом , то есть тождественно равен 0.

Достаточность. Если определитель равен 0, то какой-либо столбец линейно выражается через остальные, тогда первый элемент столбца (а ведь это и есть сама функция) является линейной комбинацией остальных функций.

Теорема 5.Существует n линейно-независимых решений линейного однородного дифференциального уравнения порядка n, и всякое другое решение есть их линейная комбинация.

Для доказательства того, что существует n линейно-независимых решений, сначала возьмём какую-либо невырожденную квадратную матрицу A порядка n.

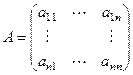
Найдётся такое решение 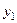, которое удовлетворяет условиям Коши:

, , , ...,

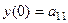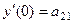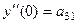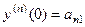
где числа взяты из 1-го столбца.

Аналогично, для чисел 2-го столбца найдётся другое частное решение 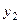, для каждого последующего тоже. Нашлось n решений. Причём это такая система функций, для которой определитель Вронского в точке 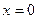равен определителю матрицы A. Ведь для и всех её производных, значения в точке 0 это и есть i-й столбец матрицы.

Определитель Вронского этой системы функций не может быть тождественно равен 0, потому что, по крайней мере, в одной точке он не равен 0. Значит, эта система ЛНС.

Всякое другое, (n+1) е решение соответствовало бы некоторым новым условиям Коши, которые можно записать в виде столбца из чисел . Но тогда обычная система линейных алгебраических уравнений

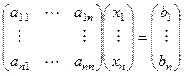
имеет единственное решение, в то же время , тогда получается, что новое решение можно как-то выразить через n ранее найденных решений.

Определение. Система из n линейно независимых решений линейного однородного дифференциального уравнения порядка n разывается фундаментальной системой решений (ФСР).

* В теореме 5 мы доказали, что линейно независимая система решений состоит ровно из n решений, не больше и не меньше. Это и есть ФСР. Она определяется не единственным образом. Если все характеристические корни различны, в качестве ФСР принимаются n различных экспонент. Если кратные корни, то в систему входят степенные функции, умноженные на экспоненту .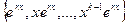

Рассмотрим подробнее, почему происходит именно так. Докажем,что если 0 является корнем кратности 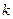, то система решений, соответствующих этому корню, имеет вид 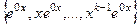, то есть . Характеристическое уравнение обязательно имеет вид 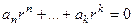, так как 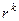можно вынести за скобку 0 корень кратности . Но это значит, что исходное дифференциальное уравнение имеет вид .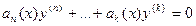

Оно содержит производные порядка 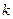и выше. Известно, что если степенную функцию продифференцировать столько раз, какова её степень, то получим константу, а если большее количество раз, то обратится в 0. Так, например,

, .

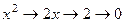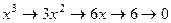В данном уравнении производные порядка и выше. Любая из степенных функций порядка 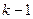и ниже, а именно взятая из набора , является решением.

Замечание. С помощью замены 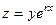доказывается, что и для произвольного ненулевого корня 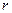верен такой же факт, то есть 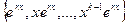, где степенные функции взяты по возрастающей, есть решения.

Линейные неоднородные дифференциальные уравнения порядка n.

В этом пункты рассмотрим уравнения такого вида: .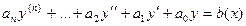

Сначала надо решать соответствующее однородное (1-й шаг). После этого для решения неоднородного уравнения есть различные способы: Лагранжа и неопределённых коэффициентов. Рассмотрим по порядку.

Обобщение метода Лагранжа для уравнений высшего порядка.

Пусть получено общее решение однородного уравнения, а именно 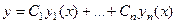. Здесь функции это как правило, экспоненты (если характеристические корни различны) либо другие типы функций, рассмотренные выше для случая кратных или комплексных корней. Теперь вместо констант запишем на этих местах неизвестные функции 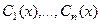, то есть решение неоднородного будем искать в виде: .

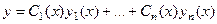Если продифференцировать 1 раз, то получим уже 2n слагаемых, после второго раза 4n, затем 8n и так далее. Получается, что в итоге у нас было бы 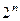слагаемых, которые подставили бы в дифференциальное уравнение, и было бы одно условие на n функций. Но для того, чтобы получить однозначное решение, можно наложить n условий на n функций, поэтому 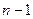условие мы можем добавить искусственно. Лагранж придумал такой способ: если приравнивать к нулю ту группу слагаемых, которая содержит 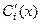на каждом этапе дифференцирования, то мы получим как раз и уменьшение количества слагаемых в следующих производных, и увеличение количества условий. Так, после 1-го дифференцирования выражения

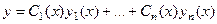получаем

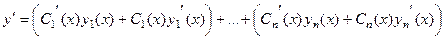
но ведь это можно перегруппировать так:

искусственно приравняем к нулю первую часть, а вторую будем дифференцировать дальше. Затем сделаем то же самое и во второй раз. Витоге к последнему разу у нас всё равно будет лишь 2n слагаемых, а вовсе не 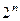. После подстановки в уравнение, а также записи всех дополнительных условий, получится система, из которой находятся неизвестные функции:

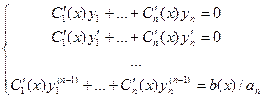
Её основная матрица точно такая же, как определитель Вронского для ранее найденной ФСР однородного уравнения.

Например, если n=2. Уравнение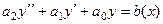

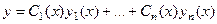
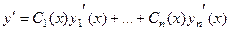(первые слагаемые, как уже было сказано, вынесли в отдельную скобку и приравняли к нулю).

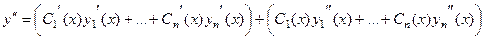На этом последнем шаге уже не приравниваем к 0, а просто подставляем в уравнение, и получим:

+ = .

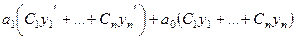Таким образом, получили выражение

.

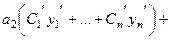
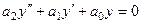так как это решение однородного уравнения.

Остаётся .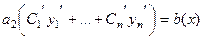

Видно, что в случае n = 2 система имеет вид:

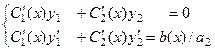
Пример. Решить методом Лагранжа уравнение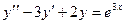

Сначала решается соответствующее однородное уравнение.

Характеристическое уравнение 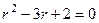. Его корни равны 1 и 2, общее решение однородного 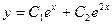. Далее вместо констант ставим неизвестные функции, то есть решение неоднородного ищем в виде 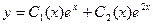. Для того, чтобы найти неизвестные функции, строим систему:

Решая её методом Гаусса, находим производные:

вычтем из 2-го уравнения 1-е, будет 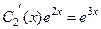, то есть 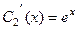. Теперь это выражение подставим в первое уравнение,

.

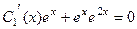
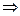
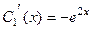Итак, , .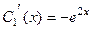

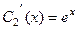Тогда

= .

= .

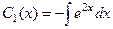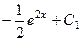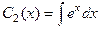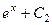Теперь подставляем их в выражение .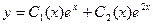

.

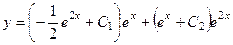Приводя подобные, в итоге получим: .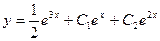

Как видим, общее решение однородного уравнения, полученное на первом шаге, выделилось в виде отдельного слагаемого. Частное решение неоднородного (слагаемое без констант), которое мы и искали методом Лагранжа, равно 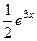. Оно очень похоже на правую часть уравнения, разве что с другим коэффициентом. На самом деле, для некоторых случаев можно обойтись без метода Лагранжа, а вид правой части определяет вид частного решения: