Пункт 1. Уравнения с разделяющимися переменными.
Уравнения вида 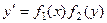 , то есть такие, в которых можно функцию разбить на отдельные множители, зависящие только от
, то есть такие, в которых можно функцию разбить на отдельные множители, зависящие только от  или только от
или только от 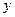 , называются уравнениями с разделяющимися переменными. К слову, далеко не все уравнения - с разделяющимися переменными. Так, если присутствует множитель
, называются уравнениями с разделяющимися переменными. К слову, далеко не все уравнения - с разделяющимися переменными. Так, если присутствует множитель 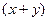 , то что бы вы ни выносили за скобку, в скобках всё равно останутся обе переменные, а не одна:
, то что бы вы ни выносили за скобку, в скобках всё равно останутся обе переменные, а не одна: 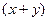 =
= 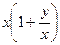 или
или 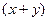 =
= 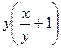 .
.
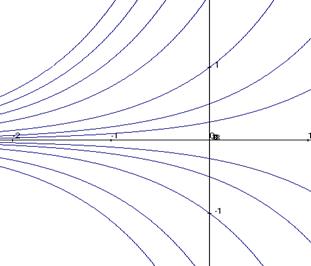
Пример. Решим уравнение 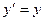 .
.
Это означает, что надо найти все такие функции, которые равны своей производной. Метод решения: сначала представить 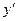 в виде
в виде 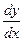 . Итак,
. Итак, 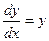 . Теперь домножим на dx, получили
. Теперь домножим на dx, получили 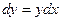 , затем разделим на
, затем разделим на 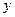 , и получили
, и получили 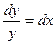 .
.
При таком делении мы неявно предполагаем, что 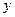 не является тождественно равной 0. Поэтому при дальнейших действиях мы упускаем случай
не является тождественно равной 0. Поэтому при дальнейших действиях мы упускаем случай 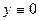 , и его надо проверить отдельно. При этом,
, и его надо проверить отдельно. При этом, 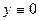 фактически является решением, подходит в уравнение
фактически является решением, подходит в уравнение 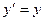 , ведь
, ведь 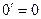 . Это называется «особым решением».
. Это называется «особым решением».
Итак, получилось следующее: 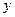 и её дифференциал с одной стороны равенства, а переменная
и её дифференциал с одной стороны равенства, а переменная  и (или) её дифференциал - с другой стороны. Теперь это выглядит так, как будто слева и справа были продифференцированы какие-то две различные функции от двух различных переменных
и (или) её дифференциал - с другой стороны. Теперь это выглядит так, как будто слева и справа были продифференцированы какие-то две различные функции от двух различных переменных 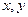 . Рассмотрим их как две независимые функции. Если теперь их проинтегрировать, то слева и справа можно получить две функции, одна от
. Рассмотрим их как две независимые функции. Если теперь их проинтегрировать, то слева и справа можно получить две функции, одна от 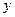 , другая от
, другая от  , а затем выразить
, а затем выразить 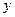 через
через  .
.
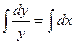
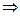
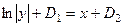 .
.
Естественно, каждый неопределённый интеграл находится с точностью до константы, поэтому там и написали  . Но можно перенести одну из констант в другую сторону равенства, и записать единую константу:
. Но можно перенести одну из констант в другую сторону равенства, и записать единую константу:
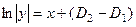 , то есть
, то есть 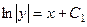 .
.
Лучше всего константу писать именно там где  , чтобы максимально очистить выражение, содержащее
, чтобы максимально очистить выражение, содержащее 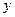 , ведь цель - выразить
, ведь цель - выразить 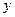 .
.
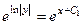
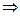
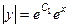 . Слева модуль, но и константа по построению является положительной,
. Слева модуль, но и константа по построению является положительной, 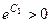 . Но надо выразить сам
. Но надо выразить сам 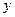 , а не его модуль, тогда справа также возможны и отрицательные константы, т.е. общее решение будет записано в виде
, а не его модуль, тогда справа также возможны и отрицательные константы, т.е. общее решение будет записано в виде 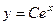 , где
, где 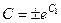 (константу для удобства переобозначили, чтобы записать ответ).
(константу для удобства переобозначили, чтобы записать ответ).
Кстати, особое решение входит сюда как частный случай, при 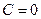 .
.
Итак, ответ: 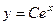 - общее решение дифф. уравнения
- общее решение дифф. уравнения 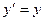 .
.
Дата добавления: 2017-05-18; просмотров: 453;
