Задача 1. Цепь с параллельными емкостями

Рассчитывается переходный процесс в рассмотренной ранее схеме (рис. 2.21). Схема и некоторые зафиксированные ранее положения здесь повторяются.

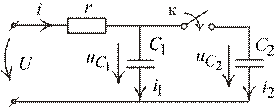Рис. 2.21

1. Старый установившийся режим.

Ключ разомкнут.

,

, .

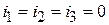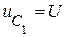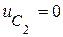Значит:

,

, .

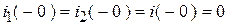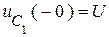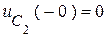2. Новый установившийся режим. Ключ замкнут.

,

.

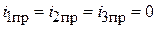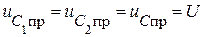3. Начальные условия.

По принципу непрерывности суммарного заряда для узла послекоммутационной схемы имеем:

,

.

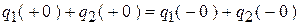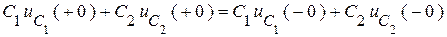В нашей схеме после мгновенной коммутации:

.

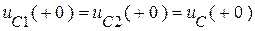Но напряжение .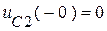

С учетом этого:

.

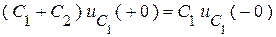Значит независимые начальные условия для напряжения :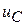

.

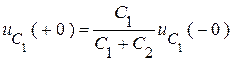В общем случае может быть зафиксирована связь:

.

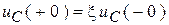В нашем примере коэффициент пропорциональности .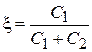

В других ситуациях он определяется содержанием схемы.

4. Постоянная интегрирования в цепи первого порядка (в послекоммутационной схеме будет чисто емкостной контур).

.

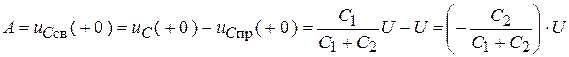5. Постоянная времени :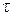

.

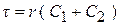6. Полное решение для напряжения на емкостях:

.

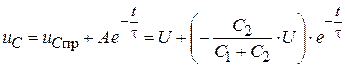7. Токи в ветвях:

,

,

.

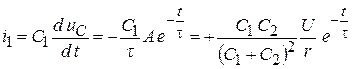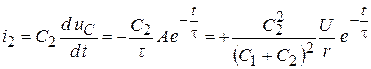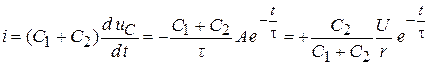Дифференцирование при расчете токов произведено без учета скачков функции 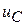в момент коммутации, поэтому результаты работают только на интервале времени .

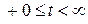На рис. 2.22 представлены графики полных производных, где эти скачки учитываются.

8. Графики функций.

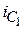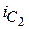Мгновенное (скачкообразное) изменение напряжений на емкостях приводит к бесконечно большим импульсам токов и в промежутке времени 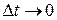. Эти равновеликие импульсы имеют разные знаки. Во входном токе 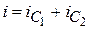во время коммутации они уничтожают друг друга и при 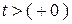просуммируются только экспоненциальные составляющие токов, организуя гладкую функцию входного тока. Площади бесконечных импульсов конечны и равны приращению зарядов 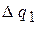и 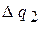на конденсаторах за время .

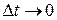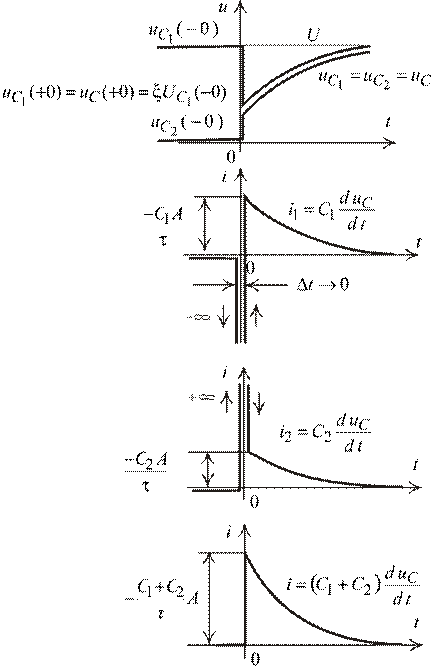Рис. 2.22

9. Некорректность мгновенной коммутации приводит к скачкообразному изменению энергии электрического поля. Энергия, запасенная в конденсаторе 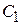до коммутации 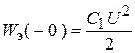больше энергии обоих конденсаторов в первый момент после коммутации :

.

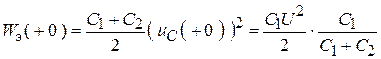Источники за время 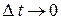не успевают обмениваться энергией с цепью. Разность энергий теряется в контакте и уходит на коротковолновое излучение.