Задача 1. Цепь с последовательными индуктивностями

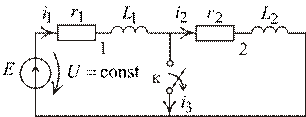Рис. 2.9

Рассчитаем переходный процесс в рассмотренной выше схеме. Схема и некоторые зафиксированные ранее положения здесь повторяются.

1. Старый установившийся режим.

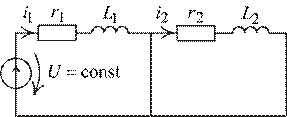Рис. 2.10

,

.

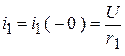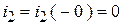2. Новый установившийся режим.

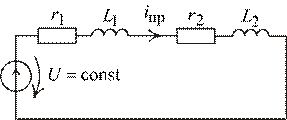Рис. 2.11

.

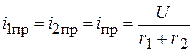3. Начальные условия:

По принципу непрерывности потокосцеплений для контура после коммутации:

;

.

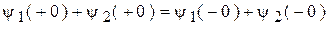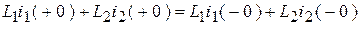Так как для схемы после мгновенной коммутации:

,

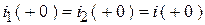а из старого установившегося режима: 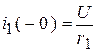и , и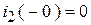меем:

,

.

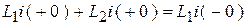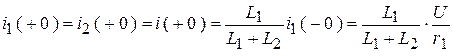В общем случае существует прямая пропорциональная связь:

.

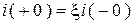В нашем примере: 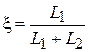. В других схемах для каждой ветви 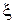определяется содержанием и структурой схемы.

Далее расчет ведется как и ранее, по обычной методике для цепей первого порядка.

4. Постоянная интегрирования:

.

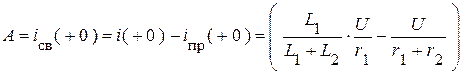5. Постоянная времени контура:

.

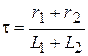6. Полное решение для тока :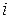

.

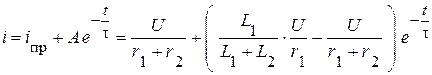7. Напряжение на индуктивностях:

,

.

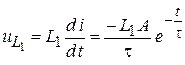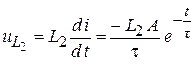Дифференцирование проведено без учета скачков тока. Поэтому эти результаты работают только справа от момента времени 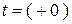на интервале .

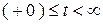Результаты дифференцирования с учетом скачков тока представлены на графиках на рис. 2.12.

Мгновенное изменение токов на индуктивностях приводит к бесконечно большим импульсам напряжений на катушке 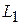и на катушке 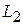в промежутке времени .

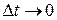Как видно, импульсы имеют противоположные знаки. Из второго закона Кирхгофа следует, что они не только противоположны по знаку, но и равновелики. ЭДС источника и токи − конечны в любой момент времени. Бесконечные импульсы напряжений должны уравновешивать друг друга. Однако интегралы от этих импульсов за промежуток времени 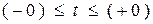конечны и равны приращением потокосцеплением катушек, что следует из вывода принципа непрерывности изменения потокосцеплений.

8. Графики переходных функций:

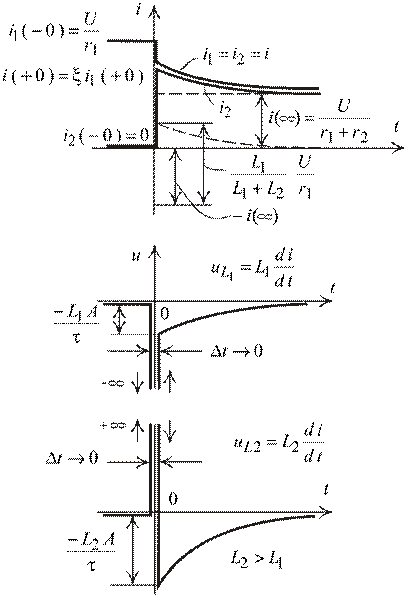Рис. 2.12

9. Отметим одно интересное свойство.

При соблюдении условия подобия параметров 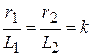, когда 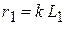и 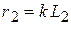постоянная интегрирования превращается в ноль:

.

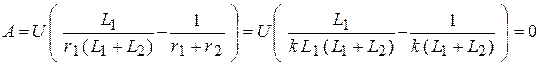Рис. 2.13

Новый установившийся режим наступает сразу после коммутации без всякого переходного процесса (рис. 2.13).

Это свойство практически можно использовать для быстрого изменения тока в индуктивности.

10. Энергетика процесса мгновенной коммутации.

Обратим внимание на то, что принцип непрерывности изменения потокосцепления не может быть получен из закона сохранения энергии. Энергия, запасенная в магнитном поле первой катушки до коммутации равна

.

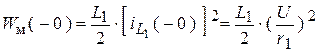Она больше энергии магнитного поля, запасенной в обеих катушках в первый момент после коммутации.

.

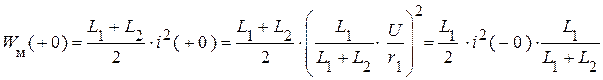Разность этих энергий расходуется на необратимые процессы за время коммутации, хотя длительность ее бесконечно мала. Эта энергия рассеивается в контакте и идет на коротковолновое излучение. Что возможно, т.к. на участках цепи развиваются мгновенные бесконечные мощности. Источник же за время бесконечно короткой коммутации не успевает обменяться энергией с цепью, поэтому в таком преобразовании энергия не участвует.