Задача 2. Цепь с параллельными индуктивностями

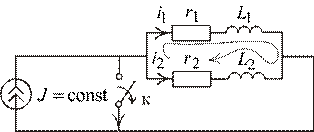Рис. 2.14

Рассчитаем переходный процесс в схеме с параллельными индуктивностями, показанной на рис. 2.14.

1. Старый установившийся режим.

.

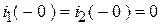2. Начальные условия:

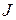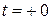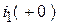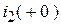Схема не может в первый момент воспринять ток , но источник ток поставляет. Следовательно, между контактами ключа возникает дуга. Если пренебречь временем горения дуги, коммутация будет некорректной. Считаем, что токи к моменту времени изменяются скачком до значений и . Запишем независимые начальные условия исходя из принципа непрерывности потокосцепления (обобщенный первый закон коммутации).

;

.

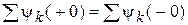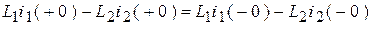Подставим известные условия: 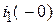, 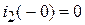и свяжем 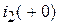с 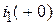по первому закону Кирхгофа.

.

.

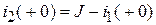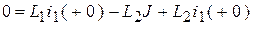Отсюда выразим начальные условия:

,

.

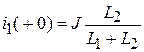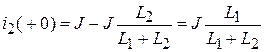3. Новый установившийся режим.

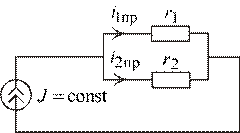Рис. 2.15

,

.

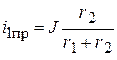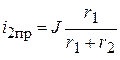4. Постоянные интегрирования в цепи первого порядка.

,

.

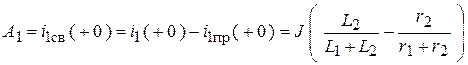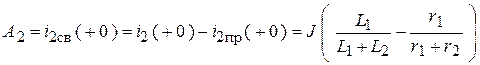5. Характеристическое уравнение и его корень.

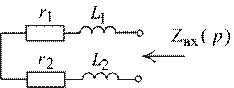Рис. 2.16

,

,

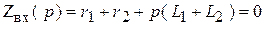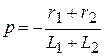Следовательно:

.

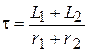6. Искомые переходные функции:

,

.

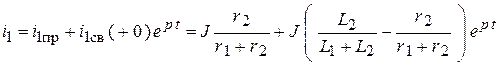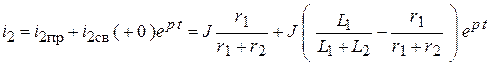7. Деформация переходного процесса в зависимости от соотношения параметров.

; ; ; ; ; ; .	; ; ; ; ; ; .	; ; ; ; ; ; .	; ; ; ; ; ; .
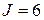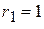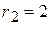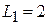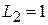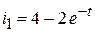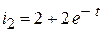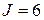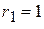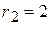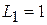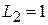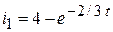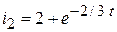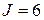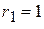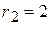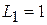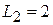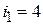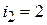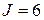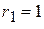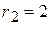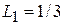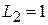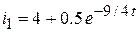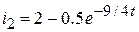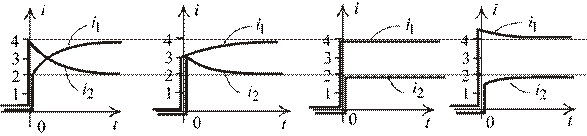
Рис. 2.17

Если соблюдается соотношение подобия параметров 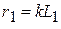и 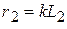, обе постоянные интегрирования превращаются в ноль.

;

.

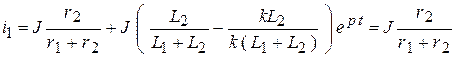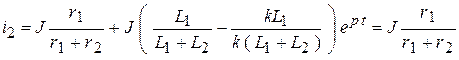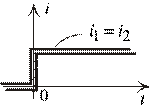Рис. 2.18

Переходного процесса нет, сразу после коммутации наступает новый установившийся режим. При этом если сопротивления 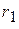и 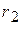одинаковы, ток источника 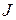делится пополам между ветвями.