Принцип непрерывности изменения потокосцепления

(или обобщенный первый закон коммутации)

1. Для определения начального значения 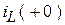в условиях некорректной коммутации, его нужно связать с известным значением 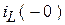. Это можно сделать, только проинтегрировав второе уравнение Кирхгофа для контура с индуктивностями послекоммутационной схемы на бесконечно малом интервале времени .

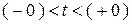2. Для рассматриваемой схемы рис. 2.7:

.

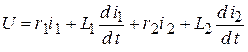Уравнение справедливо для любого момента времени, в том числе и на указанном выше интервале:

.

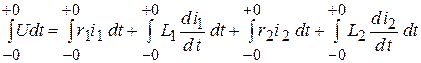Все интегралы кроме второго и четвертого слагаемых в правой части равны нулю, так как интегрирование ведется по непрерывной переменной − времени 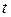. В результате остается:

.

,

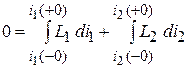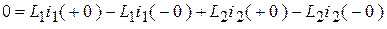или:

.

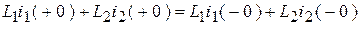В общих обозначениях:

.

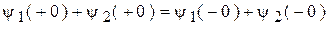или:

.

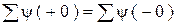Это алгебраические суммы. Правило знаков такое же, как и при формировании уравнений Кирхгофа, поскольку получены они из этих уравнений. Если обход и ток в индуктивности однонаправлены, то .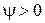

3. Итак. В замкнутом послекоммутационном контуре с индуктивностями алгебраическая сумма потокосцеплений катушек в первый момент после коммутации равна алгебраической сумме потокосцеплений в последний момент до коммутации.

Доказанное на частном примере правило распространяется на контуры с индуктивностями в любой схеме.