Задача 2. Цепь с синусоидальным источником

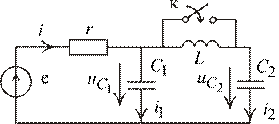Рис. 2.23

Условия:

,

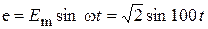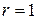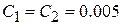(Ом), (Ф),

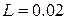( Гн).

Рассчитать переходный процесс для функции напряжения .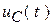

Решение:

1. Старый установившийся режим синусоидального тока.

По заданным параметрам определим:

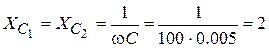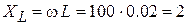(Ом),

(Ом).

В правой ветви наблюдается резонанс напряжений:

,

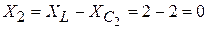значит, это короткозамкнутая ветвь.

Произведем расчет схемы в комплексах действующих значений.

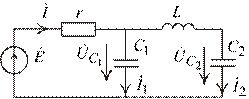Рис. 2.24

,

, .

;

;

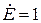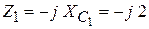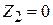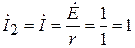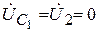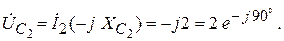
Мгновенные значения и конец старого установившегося режима:

→ ;

→ .

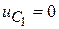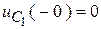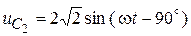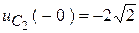2. Новый установившийся режим синусоидального тока.

Расчет схемы в комплексах действующих значений.

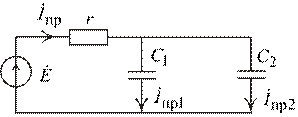Рис. 2.25

,

,

.

,

.

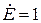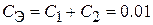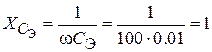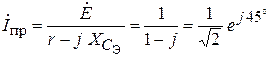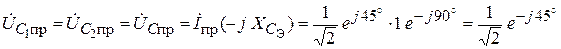Мгновенные значения:

, .

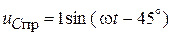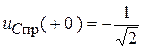3. Независимые начальные условия:

Здесь коммутационная ситуация несколько другая, чем в примере 1, однако способ расчета напряжения 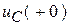тот же самый.

,

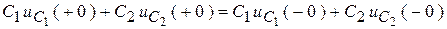Поскольку 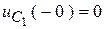, а напряжение на емкостях после мгновенной коммутации выравниваются, т.е. 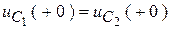, имеем:

,

.

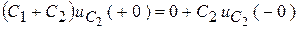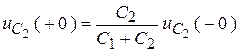Но из старого установившегося режима 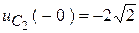, значит:

.

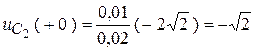4. Постоянная интегрирования в цепи первого порядка:

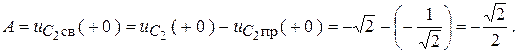
5. Постоянная времени :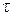

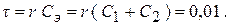
6. Полное решение для напряжения:

.

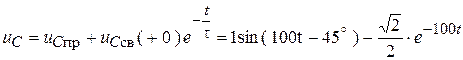Период колебаний:

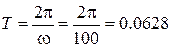с.

Длительность переходного процесса:

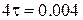с.

7. Графики функци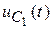й и .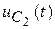

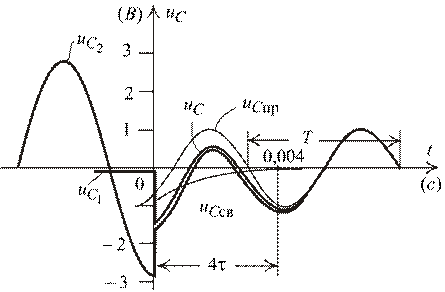Рис. 2.26

Заключение

В цепи с некорректной коммутацией, казалось бы, разрушается нечто незыблемое. Нарушаются физические законы коммутации. Ток 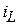и напряжение 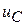в момент мгновенной коммутации меняются скачком.

Как бы нарушается закон сохранения, когда скачком меняется общий запас энергии в магнитном или электрическом поле накопителей. Поэтому, кстати, невозможно вывести из закона сохранения обобщенные законы коммутации (принцип непрерывности изменения суммарного потокосцепления и принцип непрерывности изменения суммарного заряда емкостей). Мгновенное изменение запаса энергии возможно только при затрате бесконечной мощности. Почему бы такой мощности не получиться за счет бесконечных импульсов тока 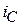и напряжения 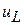? Да еще, какая то доля энергии куда-то девается в процессе мгновенной коммутации?

Все эти нарушения формальны, как формально само допущение о мгновенной коммутации. Мы смирились с некорректной коммутацией.

В цепи с некорректной коммутацией игнорируется проблематичный расчет переходного процесса на интервале времени 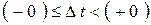. Обобщенные законы коммутации позволяют определить начальные значения тока 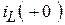и напряжения 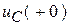для расчета постоянных интегрирования на втором этапе переходного процесса при времени .

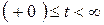В цепи с некорректной коммутацией за счет образования 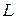−сечений и 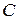−контуров понижается порядок дифференциального уравнения цепи.

Достоинства цепей с некорректной коммутацией в аспекте их расчета несомненны. Поэтому привлекательна преднамеренно организованная (путем пренебрежения малыми параметрами) некорректная коммутация в расчетной схеме цепи.

Результаты расчета так построенной задачи будут приемлемы для цепи с малыми параметрами.

Наши рассуждения прогнозируют возможные импульсные всплески напряжения 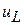и тока 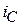в реальной цепи. Катастрофические последствия от них, должны быть блокированы соответствующими инженерными решениями.

Литература

1. Атабеков Г.И. Теоретические основы электротехники. − М.: Изд−во «Энергия», 1970. − Ч.1 −592 с.

2. Демирчян К.С., Нейман Л.Р., Коровкин Н.В., Чечурин В.Л., Теоретические основы электротехники: В 3−х т. Том 2. 4−е изд., доп. − СПб.: Питер, 2003. −576 с: ил.

3. Бессонов Л.А. Теоретические основы электротехники. Электрические цепи. − М.: Гардарики, 1999. − 638с: ил.

4. Основы теории цепей / Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. − М.: Энергоатомиздат, 1989. − 528 с.

5. Теоретические основы электротехники/ Учебник под ред. проф. П.А. Ионкина. − М.: Высшая школа, 1979. − Т.I. Основы теории линейных цепей. − 544 с.

6. Поливанов К.М. Теоретические основы электротехники. − М.: Энергия, 1972. − Ч.1 −312 с.

Содержание

Введение

Основные обозначения

Глава 1. Классический анализ переходных процессов

§1.1. Причины возникновения переходных процессов

Законы коммутации

§1.2. Общие принципы классического анализа

переходных процессов Принужденная и свободная функции

§1.3. Определение начальных условий для расчета

постоянных интегрирования

Независимые и зависимые начальные условия

§ 1.4. Способы составления характеристического уравнения

О корнях характеристического уравнения

§ 1.5. Порядок дифференциального уравнения цепи

в переходном процессе

§ 1.6. Длительность переходного процесса

Постоянная времени

§ 1.7. Переходный процесс в цепи первого порядка

§ 1.8. Примеры решения задач в цепи

первого порядка.

§1.9. Переходный процесс в цепи второго порядка

§ 1.10. Примеры решения задач в цепи второго порядка.

§1.11. Разряд конденсатора на сопротивление

и индуктивность

Глава 2. Некорректная коммутация

§ 2.1. Введение

§ 2.2. Переходные процессы в цепях с индуктивностью

§ 2.3. Принцип непрерывности изменения потокосцепления

(или обобщенный первый закон коммутации)

§ 2.4. Примеры расчета переходных процессов

в индуктивных цепях с некорректной коммутацией

§ 2.5. Переходные процессы при некорректной коммутации

в цепи с емкостями

§ 2.6. Принцип непрерывности изменения

суммарного заряда емкостей, подключенных к узлу

§ 2.7. Примера расчета переходных процессов

в емкостных цепях с некорректной коммутацией

§ 2.8. Заключение

Литература

Содержание