Формулировка критерия Гурвица

Для того чтобы система была устойчива, необходимо и достаточно, чтобы все определители Гурвица составленные из коэффициентов её характеристического уравнения были больше нуля (при a₀>0).

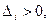i=1,n при a₀>0

Из этого критерия следует, что при n=3, необходимое и достаточное условие устойчивости имеет вид.

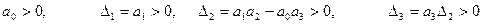
Пример используем устойчивость системы в разомкнутом и замкнутом состояниях. Характеристическое уравнение разомкнутой системы 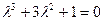. Необходимое условие не выполняется, т.к. при l коэффициент a₂=0. Поэтому разомкнутая система неустойчива.

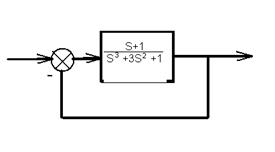
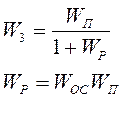
Характеристическое уравнение замкнутой системы.

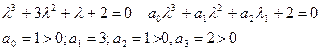
Проверим

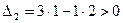Замкнутая система устойчива.

Критерий Льенара

При выполнении условия 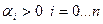для устойчивости системы необходимо и достаточно, чтобы были положительными или все определители Гурвица с четными индексами, или все определители Гурвица с нечетными индексами. Следовательно, чтобы система была устойчивой необходимо и достаточно, чтобы

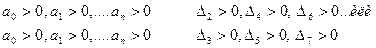
Пример. Характеристическое уравнение имеется.

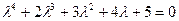
(Необходимое условие a₀>0, a₁=2>0, a₂=3>0, a₃=4>0, a₄=5>0).

Согласно критерию необходимо и достаточно 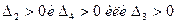Проверим выполнение более простого второго условия.

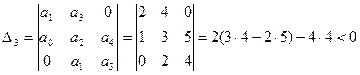
Система не устойчива.