Доказательство критерия устойчивости Найквиста
Критерий устойчивости Найквиста был разработан американским специалистом Найквистом в 1932 году. Критерий позволяет по АФХ разомкнутой системы судить об устойчивости САУ в замкнутом состоянии, при этом должно быть известно число правых корней характеристического уравнения разомкнутой системы.
Критерий устойчивости Найквиста широко используется на практике при исследовании линейных САУ. Это определяется следующим:
а) АФХ разомкнутой системы строятся гораздо проще, чем частотные характеристики замкнутой системы, поскольку в основном элементы разомкнутой системы соединены последовательно.
б) При построении АФХ разомкнутой системы могут использоваться экспериментально снятые частотные характеристики отдельных звеньев.
в) Удобно оценивать влияние разбросов (вариаций) параметров системы на её устойчивость.
Пусть передаточная функция разомкнутой системы W(p) имеет вид
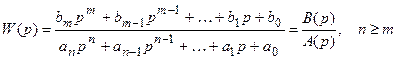 .
.
Рассмотрим вспомогательную функцию
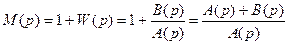 ,
,
где 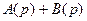 – полином числителя, определяющий характеристическое уравнение замкнутой системы с корнями ni, i=1, 2, …, n.
– полином числителя, определяющий характеристическое уравнение замкнутой системы с корнями ni, i=1, 2, …, n.
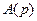 – полином знаменателя, определяющий характеристическое уравнение разомкнутой системы с корнями li, i=1, 2, …, n.
– полином знаменателя, определяющий характеристическое уравнение разомкнутой системы с корнями li, i=1, 2, …, n.
На основании теоремы Безу имеем
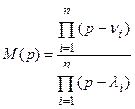 .
.
Для устойчивости замкнутой системы необходимо и достаточно, чтобы все корни ni, i=1, 2, ..., n были левыми, при этом разомкнутая система в общем случае может быть и неустойчивой.
Подставляя p=jw, переходим к частотным характеристикам.
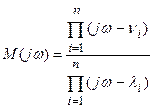 .
.
Для доказательства критерия воспользуемся принципом аргумента, считая, что все корни характеристического уравнения замкнутой САУ ni, i=1, 2, ..., n – левые, а среди n корней характеристического уравнения разомкнутой системы li, i=1, 2, ..., n имеется “l” правых корней.
Найдем приращение аргумента функции M(jw) при изменении частоты от 0 до ¥. Это связано с тем, что функция M(jw) при изменении w от –¥ до 0 является зеркальным отображением этой функции относительно оси абсцисс при изменении w от 0 до ¥. Поэтому строится только одна ветвь этой характеристики для частот от 0 до ¥.
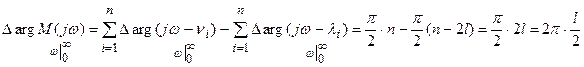 .
.
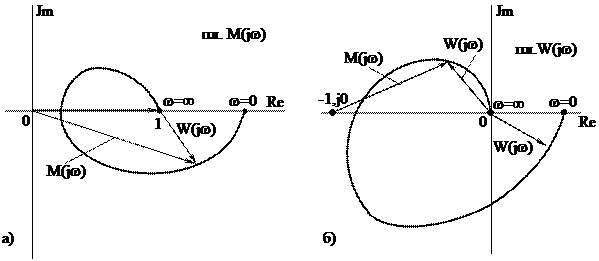 Таким образом, если замкнутая система устойчива, а разомкнутая система неустойчива и имеет l правых корней, то вектор M(jw) должен повернуться вокруг начала координат на угол
Таким образом, если замкнутая система устойчива, а разомкнутая система неустойчива и имеет l правых корней, то вектор M(jw) должен повернуться вокруг начала координат на угол 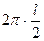 в положительном направлении.
в положительном направлении.
Рис. 10.1
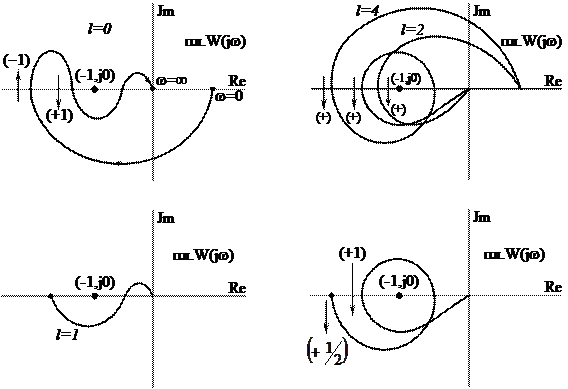 |
Рис. 10.2
Если ось ординат плоскости M(jw) сместить на единицу вправо, то становится очевидным, что охвату вектором M(jw) начала координат соответствует охват вектором W(jw) точки (-1, j0), которую называют критической точкой.
На основании этого можно сформулировать критерий устойчивости Найквиста:
“Для устойчивости САУ в замкнутом состоянии необходимо и достаточно, чтобы АФХ разомкнутой системы W(jw) при изменении частоты от 0 до ¥ охватывала критическую точку (-1, j0) в положительном направлении 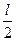 раз, где l – число правых корней характеристического уравнения разомкнутой системы”.
раз, где l – число правых корней характеристического уравнения разомкнутой системы”.
Этот критерий удобно сформулировать по числу переходов: для устойчивости САУ в замкнутом состоянии необходимо и достаточно, чтобы разность между числом положительных и отрицательных переходов АФХ разомкнутой системы через отрезок вещественной оси (-1, -¥) при изменении частоты от 0 до ¥ была равна 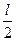 , где l – число правых корней характеристического уравнения разомкнутой системы (см. рис. 10.2).
, где l – число правых корней характеристического уравнения разомкнутой системы (см. рис. 10.2).
2. Применение критерия устойчивости Найквиста для астатических систем
Выражение для передаточной функции астатической системы n-го порядка имеет вид:
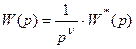 .
.
Подставляя p=jw, получаем
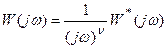 ,
,
где W*(jw) не содержит интегрирующих звеньев.
 В точке w=0 характеристика W(jw) терпит разрыв непрерывности и её характер становится неопределенным. Для того чтобы избежать этого, будем обходить точку w=0 по окружности бесконечно малого радиуса против часовой стрелки.
В точке w=0 характеристика W(jw) терпит разрыв непрерывности и её характер становится неопределенным. Для того чтобы избежать этого, будем обходить точку w=0 по окружности бесконечно малого радиуса против часовой стрелки.
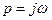 ,
, 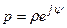 где
где 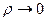 , а
, а 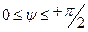
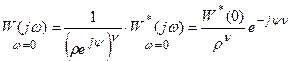 ,
,
если 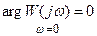 .
.
Это означает, что характеристика W*(jw) дополняется дугой бесконечного радиуса на угол 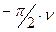 .
.
После этого к полученной АФХ разомкнутой системы критерий устойчивости Найквиста применяют без каких-либо изменений.
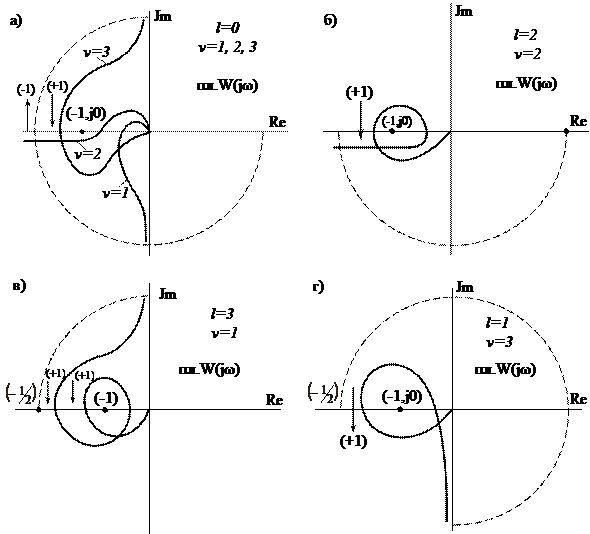 |
Рис. 10.4
4. Запасы устойчивости систем
А. Критерий Михайлова. Кривая Михайлова для устойчивой системы, как известно, не должна проходить через начало координат. Удаление этой кривой от начала координат и будет характеризовать запас устойчивости системы по этому критерию. Система автоматического управления будет иметь запас устойчивости не менее а>0, если соответствующая ей кривая Михайлова не будет пересекать окружность с центром в начале координат и радиусом, равным а (рис.10.5).
Условие выхода системы на границу устойчивости по критерию Михайлова имеет вид:
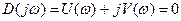 .
.
Это условие может быть записано так:
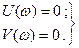 (9.1)
(9.1)
Уравнения (10.1) могут быть использованы для определения критических значений параметров системы.
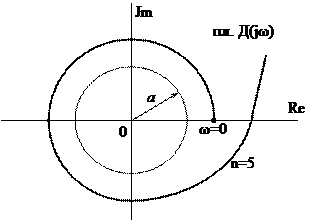 |
Рис.10.5. Запасы устойчивости САУ по кривой Михайлова.
Б. Критерий Найквиста. Запасы устойчивости САУ по критерию Найквиста определяются удалением АФХ разомкнутой системы от критической точки (-1, j0). На рис.10. изображена АФХ разомкнутой системы W(jw) и показаны запасы устойчивости по фазе jз и по амплитуде аз. Запасы устойчивости вычисляются так:
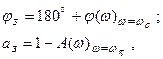
где 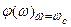 – значение фазо-частотной характеристики разомкнутой системы при w=wс, А(wс)=1;
– значение фазо-частотной характеристики разомкнутой системы при w=wс, А(wс)=1;
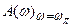 – значение амплитудно-частотной характеристики разомкнутой системы при w=wp , j(w)=p.
– значение амплитудно-частотной характеристики разомкнутой системы при w=wp , j(w)=p.
 |
Запас устойчивости системы по амплитуде может характеризоваться значением А(wp), при этом, очевидно, что с уменьшением А(wp) возрастает запас устойчивости системы
Рис.10.6. Запасы устойчивости САУ по критерию Найквиста
по амплитуде.
САУ будет находиться на границе устойчивости, если АФХ разомкнутой системы будет проходить через критическую точку (-1,j0). Это условие для 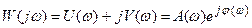 записывается так:
записывается так:
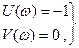 или
или 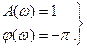 (10.2)
(10.2)
Полученные уравнения (10.2) могут быть использованы для определения критических значений параметров системы.
3. Управляемость и наблюдаемость
| <== предыдущая лекция | | | следующая лекция ==> |
| | | Методика построения логарифмических частотных характеристик разомкнутой САУ. |
Дата добавления: 2016-06-24; просмотров: 2228;
